Learned Threshold Token Merging and Pruning for Vision Transformers
Abstract
Vision transformers have demonstrated remarkable success in a wide range of computer vision tasks over the last years. However, their high computational costs remain a significant barrier to their practical deployment. In particular, the complexity of transformer models is quadratic with respect to the number of input tokens. Therefore techniques that reduce the number of input tokens that need to be processed have been proposed. This paper introduces Learned Thresholds token Merging and Pruning (LTMP), a novel approach that leverages the strengths of both token merging and token pruning. LTMP uses learned threshold masking modules that dynamically determine which tokens to merge and which to prune. We demonstrate our approach with extensive experiments on vision transformers on the ImageNet classification task. Our results demonstrate that LTMP achieves state-of-the-art accuracy across reduction rates while requiring only a single fine-tuning epoch, which is an order of magnitude faster than previous methods.
TL;DR
 |
+ |
 |
= |
 |
|---|
Method
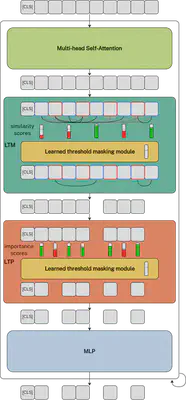
Overview
An overview of our framework is shown below. Given any vision transformer, our approach adds merging (LTM) and pruning (LTP) components with learned threshold masking modules in each transformer block between the Multi-head Self-Attention (MSA) and MLP components. Based on the attention in the MSA, importance scores for each token and similarity scores between tokens are computed.
Learned threshold masking modules then learn the thresholds that decide which tokens to prune and which ones to merge.
Learned thresholds
Learned thresholds pruning
In each transformer block an importance score is calculated for every token $\mathbf{x}_i, i \in {1,…,n}$, where $n = h w$ is the number of tokens1. A threshold $\theta^l \in \mathbb{R}, l \in {1,…,L}$, where $L$ is the number of transformer blocks, determines which tokens to keep and which to prune in each layer; only tokens with an importance score above the threshold are kept.
In order to prune tokens adaptively, we introduce a threshold masking module that, given the importance scores $\mathbf{s}^l \in \mathbb{R}^n$, learns a pruning threshold $\theta^l$ and outputs which tokens to keep. \begin{equation} M(\mathbf{s}^l_i, \theta^l) = \begin{cases} 1, &\text{if }\mathbf{s}^l_i > \theta^l\ 0, &\text{otherwise} \end{cases} \end{equation}
However, in order to make $\theta^l$ learnable during training, the threshold masking module needs to be differentiable. We achieve this by implementing the threshold masking module as a straight-through estimator (Bengio et al., 2013), where we estimate the masking function during backpropagation as \begin{equation} M(\mathbf{s}^l_i, \theta^l) = \sigma(\frac{\mathbf{s}^l_i - \theta^l}{\tau}) \end{equation} where $\sigma(x)$ is the sigmoid function and $\tau$ is the temperature hyperparameter.
During inference we only keep the tokens in the $l$-th block where $M(\mathbf{s}^l_i, \theta^l) = 1$. However, during training, we can not simply drop tokens as that does not allow the model to backpropagate the influence of the threshold on the model performance. We, therefore, create a mask indicating which tokens are kept and which ones are pruned. Every threshold masking module only updates the entries of the mask for the tokens that have not yet been removed prior to that layer, as tokens that are pruned in an earlier layer have to remain pruned. We construct the pruning mask $\mathbf{m}^l \in [0,1]^n$ as follows: \begin{equation} \mathbf{m}^l_i = \begin{cases} M(\mathbf{s}^l_i, \theta^l), &\text{if } \mathbf{m}^{l-1}_i = 1\ \mathbf{m}^{l-1}, &\text{otherwise} \end{cases} \end{equation}
To implement the effect of pruning with a mask during the forward pass, our approach makes changes to the only place where tokens influence each other: the attention mechanism2.
Recall the original formula for attention (Vaswani et al., 2017): \begin{equation} \operatorname{Attention}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = \operatorname{softmax}(\frac{\mathbf{QK}^T}{\sqrt{d_k}})\mathbf{V} \end{equation}
In order to avoid that the masked tokens influence the attention mechanism, we propose a modified function: \begin{equation} \operatorname{Attention-with-mask}(\mathbf{Q}, \mathbf{K}, \mathbf{V}, \mathbf{m}) = \mathbf{S}\mathbf{V} \end{equation} where,
\begin{equation} \mathbf{S}_{ij} = \frac{\exp(\mathbf{A}_{ij})\mathbf{m}_{j}}{\sum_{k=1}^N\exp(\mathbf{A}_{ik})\mathbf{m}_{k}}, 1\le i,j,k\le n \end{equation}
and, \begin{equation} \mathbf{A} = \mathbf{Q}\mathbf{K}^T/\sqrt{d_k} \in \mathbb{R}^{n\times n} \end{equation} $\operatorname{Attention-with-mask}$ computes a masked softmax, which is equivalent to a softmax calculated with the pruned tokens removed. $\operatorname{Attention-with-mask}$ is conceptually similar to the masked attention as found in the transformer decoder of language models. However, where the masking in transformer decoders is done by setting masked tokens to $-\infty$, our approach requires the influence of the straight-through estimator mask to propagate to the thresholds during backpropagation.
Learned thresholds merging
Token merging (ToMe) (Bolya et al., 2023) is originally a top-$k$ approach, meaning that it merges based on a fixed rate and has no learnable parameters. We modify ToMe to use thresholds instead of top-$k$ by applying the same techniques as introduced in the previous section; this is by adding our learned threshold masking module, in which similarity scores above these thresholds are selected for merging, and by changing the attention function to $\operatorname{Attention-with-mask}$.
Learned thresholds merging and pruning
With learnable thresholds, it is trivial to combine merging and pruning, as we can simply add a learned threshold masking module that learns thresholds for importance scores and another module that learns thresholds for similarity scores.
Training Strategy
Training objective
To effectively reduce the number of tokens in the transformer blocks, it is necessary to include a regularization loss term in the training process. Without this loss, the model has no incentive to prune any tokens and the pruning thresholds will simply be set to $0$ as the most accurate model uses all inputs. We propose a budget-aware training loss which introduces a reduction target $r_{\text{target}}$ for the FLOPs of the vision transformer.
Let us denote $\phi_{\text{module}}(n,d)$ as a function that calculates the FLOPs of a module based on the number of tokens $n$ and the embedding dimension $d$. The actual FLOPs reduction factor $r_{\text{FLOPs}}$ of a ViT can then be computed as: \begin{equation} r_{\text{FLOPs}} = \frac{\phi_{\text{PE}}(n,d)}{\phi_{\text{ViT}}(n,d)} + \sum_{l=1}^L \frac{\phi_{\text{BLK}}(n,d)}{\phi_{\text{ViT}}(n,d)}\left(\frac{\phi_{\text{MSA}}(\bar{\mathbf{m}}^{l-1}n,d)}{\phi_{\text{BLK}}(n,d)} + \frac{\phi_{\text{MLP}}(\bar{\mathbf{m}}^{l}n,d)}{\phi_{\text{BLK}}(n,d)}\right) + \frac{\phi_{\text{HEAD}}(\bar{\mathbf{m}}^{l}n,d)}{\phi_{\text{ViT}}(n,d)} \end{equation} where $\bar{\mathbf{m}}^l = \frac{1}{n}\sum_{i=1}^n \mathbf{m}^l_i$ is the percentage of input tokens that are kept after the $l$-th threshold masking operation and $\bar{\mathbf{m}}^0 = 1$. PE, BLK and HEAD denote the different components of a vision transformer: the patch embedding module, the transformer blocks and the classification head.
As the vast majority of the FLOPs in a vision transformer occurs in the transformer blocks ($\approx 99 %$ percent in ViT-S), we ignore the FLOPs in the patch embedding and classification head: $\frac{\phi_{\text{PE}}(n,d)}{\phi_{\text{ViT}}(n,d)} = \frac{\phi_{\text{HEAD}}(n,d)}{\phi_{\text{ViT}}(n,d)} \approx 0$. That means that we can simplify \begin{equation}\label{eq:approx_blk} \frac{\phi_{\text{BLK}}(n,d)}{\phi_{\text{ViT}}(n,d)} \approx \frac{1}{L}, \end{equation} where $L$ is the number of transformer blocks.
The FLOPs of a transformer block and its two components, the MSA and MLP can be computed as: \begin{equation}\label{eq:MSA} \phi_{\text{MSA}}(n,d) = 4nd^2 + 2n^2d \end{equation} \begin{equation}\label{eq:MLP} \phi_{\text{MLP}}(n,d) = 8nd^2 \end{equation} \begin{equation}\label{eq:BLK} \phi_{\text{BLK}}(n,d) = \phi_{\text{MSA}}(n,d) + \phi_{\text{MLP}}(n,d) = 12nd^2+2n^2d \end{equation}
Combining the above equations gives: \begin{equation}\label{eq:reduction_flops} r_{\text{FLOPs}} \approx{} \sum_{l=1}^L \frac{1}{L}\left(\frac{2\bar{\mathbf{m}}^{l-1}nd^2 + (\bar{\mathbf{m}}^{l-1}n)^2d + 4\bar{\mathbf{m}}^{l}nd^2}{6nd^2 + n^2d}\right) \end{equation}
Given this FLOPs reduction factor $r_{\text{FLOPs}}$ as a function of the threshold masks, we define our regularization loss as the squared error between the reduction target and the actual FLOPs reduction factor: \begin{equation} \mathcal{L}_{\text{reg}} = (r_{\text{target}} - r_{\text{FLOPs}})^2 \end{equation} This regularization loss is then combined with the classification loss, for which we adopt the standard cross entropy loss. \begin{equation} \mathcal{L} = \mathcal{L}_{\text{CE}} + \lambda \mathcal{L}_{\text{reg}} \end{equation} The overall training objective is to learn thresholds that optimize the model while reducing the model complexity to a certain reduction target. The combination of learned thresholds and our budget-aware loss enables the model to optimally distribute merging and pruning across layers.
Training schedule
LTMP only adds two learnable parameters per transformer block (one for pruning and one for merging). As is common in pruning it is applied to pretrained models. We therefore only update the thresholds during training and keep all other trainable parameters fixed, allowing LTMP to converge within a single epoch.
Results
DeiT
|
|
|
|
|---|
ViT
Comparison to other pruning works
| Method | FLOPs | Accuracy | fine-tune epochs |
|---|---|---|---|
| DeiT-S (Baseline) | 4.6G | 79.8 | - |
| SPViT | 3.8G | 79.8 | 75 |
| LTMP (Ours) | 3.8G | 79.8 | 1 |
| DynamicViT | 2.9G | 79.3 | 30 |
| EViT | 3.0G | 79.5 | 30 |
| EViT | 3.0G | 79.8 | 100 |
| Evo-ViT | 3.0G | 79.4 | 300 |
| ToMe | 3.0G | 79.3 | 0 |
| LTMP (Ours) | 3.0G | 79.6 | 1 |
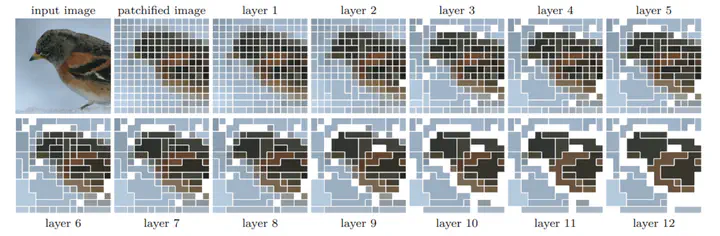
Visualizations
| input | layer 1 | layer 2 | layer 3 | layer 4 | layer 5 | layer 6 | layer 7 | layer 8 | layer 9 | layer 10 | layer 11 | layer 12 |
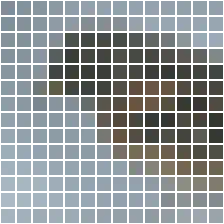 |
 |
 |
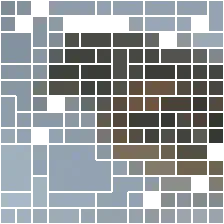 |
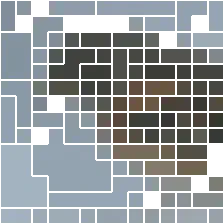 |
 |
 |
 |
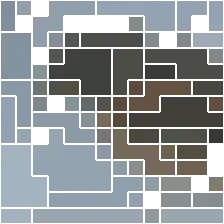 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
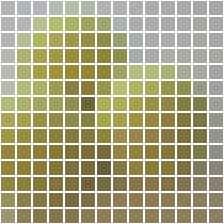 |
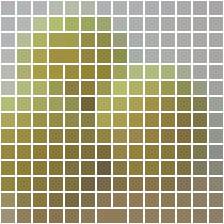 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Citation
@inproceedings{
bonnaerens2023learned,
title={Learned Thresholds Token Merging and Pruning for Vision Transformers},
author={Maxim Bonnaerens and Joni Dambre},
booktitle={Workshop on Efficient Systems for Foundation Models @ ICML2023},
year={2023},
url={https://openreview.net/forum?id=19pi10cY8x}
}
-
We omit the
[CLS]class token for simplicity, during pruning and/or merging we always keep the[CLS]token. ↩︎ -
Technically, tokens also influence each other during layer normalization, however as pruning is done on pretrained models, we simply use the global statistics from pretraining during normalization. ↩︎