How are the 3D Gaussians parameterized in 3D Gaussian Splatting?
The anisotropic 3D gaussians are modeled using a scale vector \(s \in \mathbb{R}^3\) and quaternions \(q\).
From this the scaling matrix \(S\) and rotatation matrix \(R\) can be constructed.
The typical parameterization of a guassian through a covariance matrix can then be obtained as:
\[\Sigma = RSS^TR^T\]
From this the scaling matrix \(S\) and rotatation matrix \(R\) can be constructed.
The typical parameterization of a guassian through a covariance matrix can then be obtained as:
\[\Sigma = RSS^TR^T\]
To avoid overhead they also explicitly derive the gradients of these parameters.
Give a schematic overview of the 3D Gaussian Splatting method.
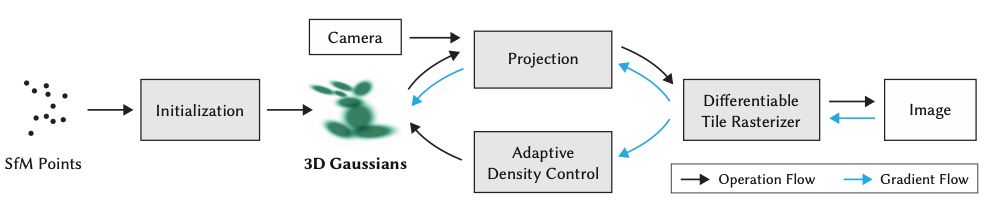
How is color parameterized in 3D Gaussian Splatting?
Using spherical harmonics, this allows the color of a gaussian to be different based on the viewing direction.
How are the initial 3D gaussians obtained in 3D gaussian splatting?
They are taken from SfM (Structure-from-motion) that is ran prior to 3D Gaussian Splatting. SfM also provides the camera parameters for each image.
The authors show that using randomly initialized gaussians perform much worse.
Which parameters of the 3D gaussian are optimized in 3D Gaussian Splatting?
The 3D position of the guassian, the properties of the anisotropic gaussian (through scale and rotation), the \(\alpha\) for the \(\alpha\)-blending and the spherical harmonics coefficients.