Which aspects of NeRF does instant-ngp improve?
1. Rendering algorithm: They accelerate the ray sampling by skipping over the empty space and stopping after enough density has been reached, this is done using occupancy grids.
2. Small neural network: NeRFs only require small neural networks, by implementing them in a single cuda kernel they improve 10x over PyTorch/Tensorflow. (https://github.com/NVlabs/tiny-cuda-nn)
3. A faster input encoder: They introduce a multi-resolution hash encoding to encode the neural network inputs in a faster and more accurate manner. This is the main contribution of the paper.
2. Small neural network: NeRFs only require small neural networks, by implementing them in a single cuda kernel they improve 10x over PyTorch/Tensorflow. (https://github.com/NVlabs/tiny-cuda-nn)
3. A faster input encoder: They introduce a multi-resolution hash encoding to encode the neural network inputs in a faster and more accurate manner. This is the main contribution of the paper.
Give an overview of the multiresolution hash encoding introduced in instant-ngp.
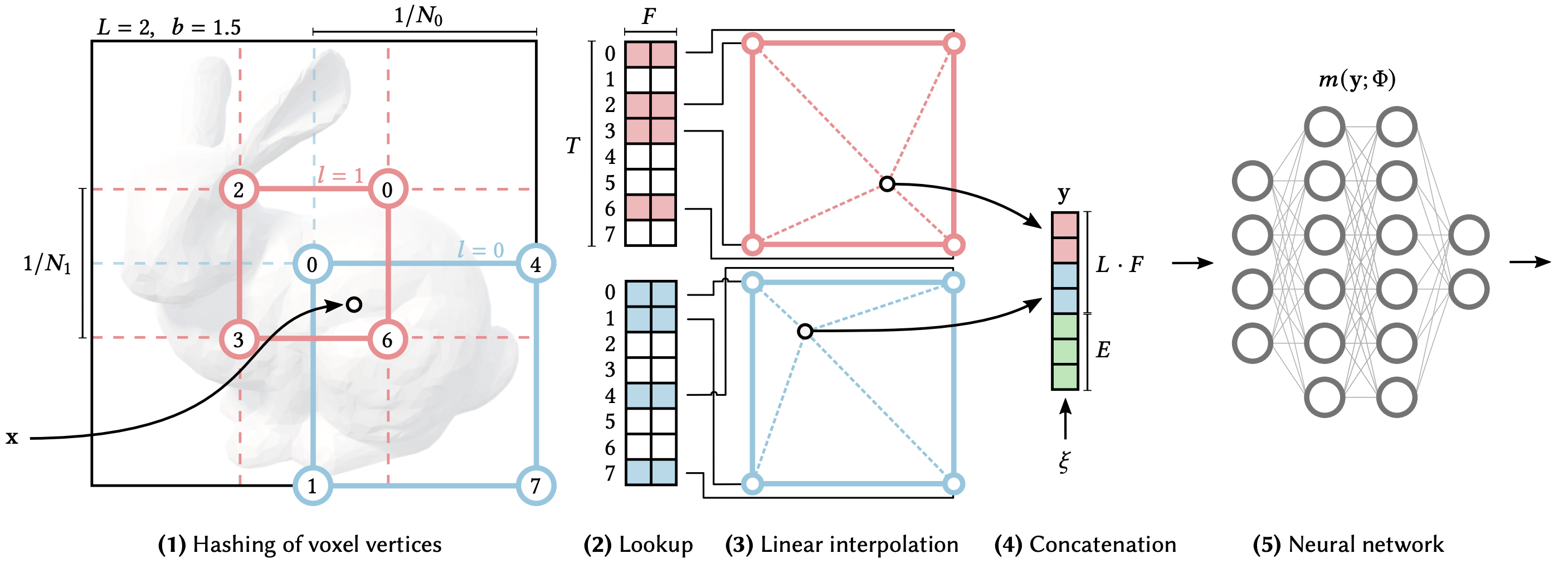
(1) for a given input coordinate \(\mathbf{x}\), we find the surrounding voxels at \(L\) resolution levels and assign indices to their corners by hashing their integer coordinates.
(2) for all resulting corner indices, we look up the corresponding \(F\)-dimensional feature vectors from the hash-tables \(\theta_l\)
and (3) linearly interpolate them according to the relative position of \(\mathbf{x}\) within the respective \(l\)-th voxel.
(4) we concatenate the result of each level, as well as auxiliary inputs \({\xi \in \mathbb{R}^E}\), producing the encoded MLP input \({y \in \mathbb{R}^{LF+E}}\), which (5) is evaluated last.
To train the encoding, loss gradients are backpropagated through the MLP (5), the concatenation (4), the linear interpolation (3), and then accumulated in the looked-up feature vectors.
How is an input coordinate \(\mathbf{x} \in \mathbb{R}^d \) mapped to \(L\) voxels in instant-ngp?
The \(L\) voxels represent the different resolutions \(N_l\) between the coarsest and finest resolutions \([N_\min, N_\max]\):
\[b = \exp(\frac{\ln(N_\max) - \ln(N_\min)}{L-1})\]\[N_l = \lfloor N_\min \cdot b^l \rfloor\]The voxel corners are then located at \(\lfloor\mathbf{x}\cdot N_l\rfloor\) and \(\lceil\mathbf{x}\cdot N_l\rceil\).
\[b = \exp(\frac{\ln(N_\max) - \ln(N_\min)}{L-1})\]\[N_l = \lfloor N_\min \cdot b^l \rfloor\]The voxel corners are then located at \(\lfloor\mathbf{x}\cdot N_l\rfloor\) and \(\lceil\mathbf{x}\cdot N_l\rceil\).
Which hash function is used in the multiresolution hash encoding of instant-ngp?
They use the spatial hash function of the form:
\[h(\mathbf{x}) = \left(\bigoplus_{i=1}^{d} x_i \pi_i \right) \mod T\]where \(\oplus\) denotes the bit-wise XOR operation and \(\pi_i\) are unique, large prime numbers.
\[h(\mathbf{x}) = \left(\bigoplus_{i=1}^{d} x_i \pi_i \right) \mod T\]where \(\oplus\) denotes the bit-wise XOR operation and \(\pi_i\) are unique, large prime numbers.
Effectively, this formula XORs the results of a per-dimension linear congruential (pseudo-random) permuation, decorrelating the effect of the dimensions on the hashed value.
How is the viewing direction encoded in multiresolution hashing of instant-ngp?
All inputs besides the input coordinates are concatenated to the multiresolution hashed input coordinates.
How are hash collisions handled in the multiresolution hash encoding of instant-ngp?
There is no collision handling.
They rely on the neural network to be robust against hash collision. One reason this works is because the coarsers levels fit in the hashtable and have no collisions and the higher resolutions are statistically unlikely to have collisions simultaneously at many levels.
They rely on the neural network to be robust against hash collision. One reason this works is because the coarsers levels fit in the hashtable and have no collisions and the higher resolutions are statistically unlikely to have collisions simultaneously at many levels.