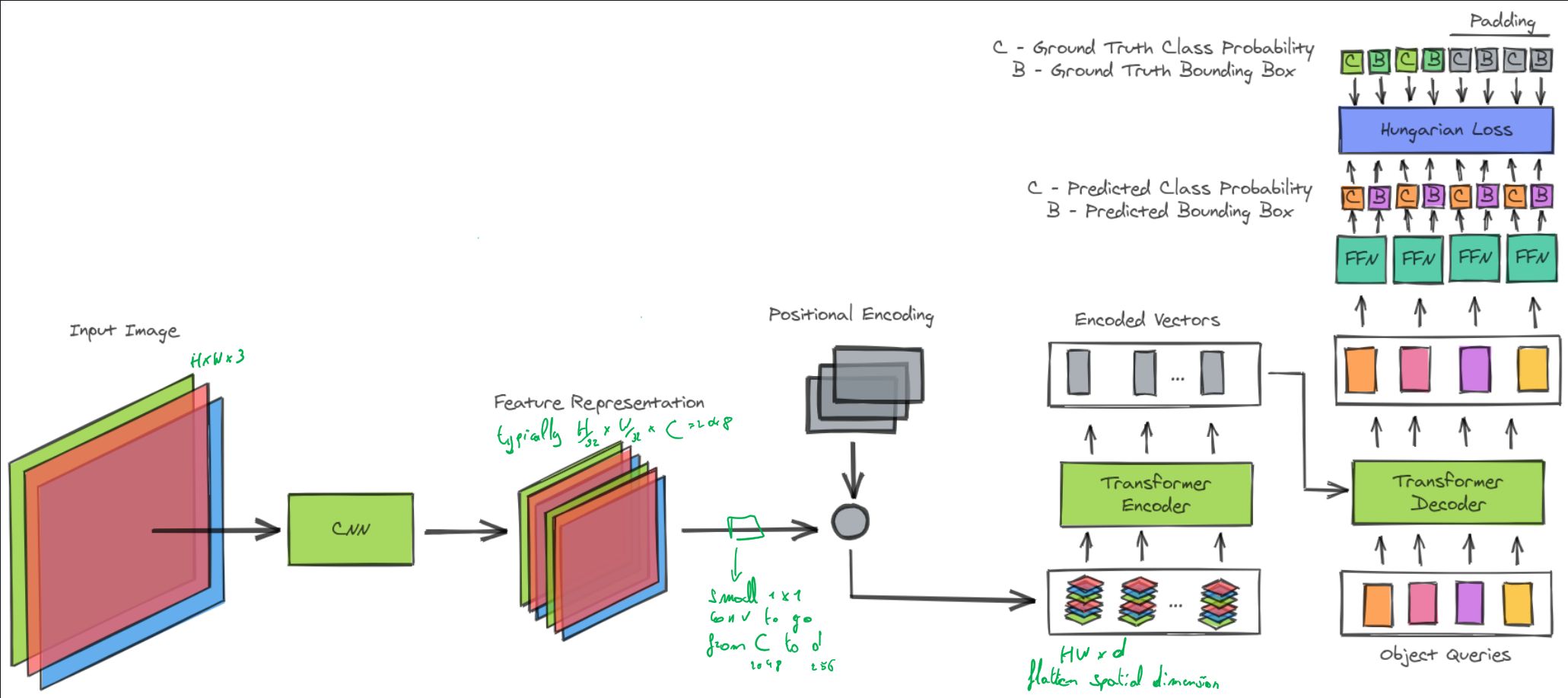
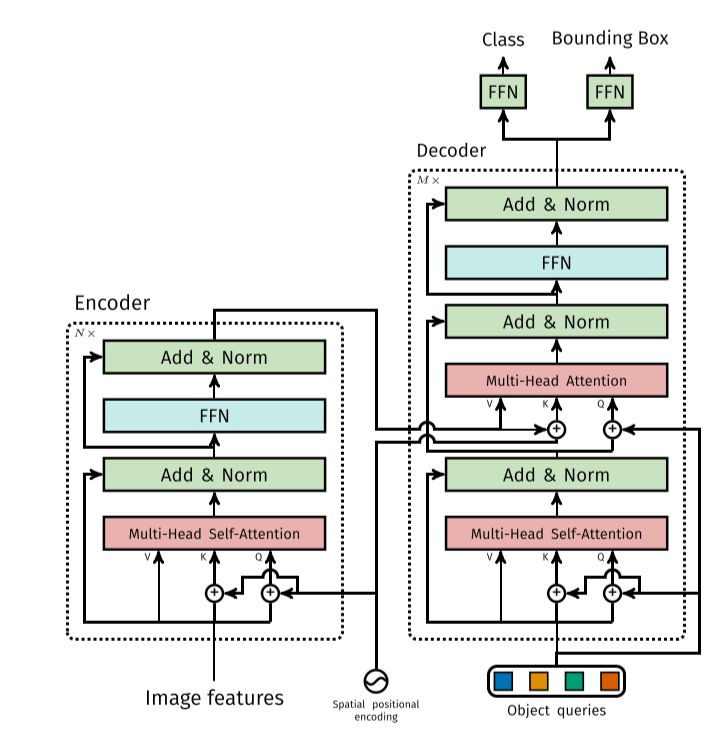
Draw the architecture of DETR.
While DETR has a better AP than previous CNN based object detection algorithms, in which aspects is it worse than those models?
DETR performs worse on small objects.
DETR requires extra-long training.
DETR requires extra-long training.
Why is DETR called an End-to-End detector?
DETR predicts all objects at once, without an intermediate step such as non-maximal suppression.
This is done using a set loss function which performs bipartite matching between predicted and ground-truth objects.
How does DETR match predictions with ground-truth?
DETR uses bipartite matching between predicted and ground truth objects.
Assuming \(N\) is larger than the number of objects in the image,
we consider \(y\) also as a set of size \(N\) padded with \(\emptyset\) (no object).
To find a bipartite matching between these two sets we search for a permutation of \(N\) elements \(\sigma \in \Sigma_N\) with the lowest cost:
\[\hat{\sigma} = \text{argmin}_{\sigma\in\Sigma_N} \sum_{i}^{N} L_{match}(y_i, \hat{y}_{\sigma(i)}),\]
where \(\cal{L}_{match}(y_i, \hat{y}_{\sigma(i)})\) is a pair-wise matching cost between ground truth \(y_i\) and a prediction with index \(\sigma(i)\).
This optimal assignment is computed efficiently with the Hungarian algorithm.
This optimal assignment is computed efficiently with the Hungarian algorithm.
The matching cost takes into account both the class prediction and the similarity of predicted and ground truth boxes. Each element \(i\) of the ground truth set can be seen as a \(y_i = (c_i, b_i)\) where \(c_i\) is the target class label (which may be \(\emptyset\)) and \(b_i \in [0, 1]^4\) is a vector that defines ground truth box center coordinates and its height and width relative to the image size. For the prediction with index \(\sigma(i)\) we define probability of class \(c_i\) as \(\hat{p}_{\sigma(i)}(c_i)\) and the predicted box as \(\hat{b}_{\sigma(i)}\). With these notations we define
\(\cal{L}_{match}(y_i, \hat{y}_{\sigma(i)})\) as \(-\mathbb{1}_{\{c_i\neq\emptyset\}}\hat{p}_{\sigma(i)}(c_i) + \mathbb{1}_{\{c_i\neq\emptyset\}} \cal{L}_{box}(b_{i}, \hat{b}_{\sigma(i)})\).
Which loss function is used in DETR?
The Hungarian loss.
Which is a linear combination of a negative log-likelihood for class prediction and a box loss:
\[\cal{L}_{Hungarian}(y, \hat{y}) = \sum_{i=1}^N \left[-\log \hat{p}_{\hat{\sigma}(i)}(c_{i}) + \mathbb{1}_{\{c_i\neq\emptyset\}} \cal{L}_{box}(b_{i}, \hat{b}_{\hat{\sigma}}(i))\right]\]
where
\[\cal{L}_{box}(b_{i}, \hat{b}_{\hat{\sigma}}(i)) = \lambda_{\rm iou}\cal{L}_{iou}(b_{i}, \hat{b}_{\sigma(i)}) + \lambda_{\rm L1}||b_{i}- \hat{b}_{\sigma(i)}||_1 \]
with \(\cal{L}_{iou}\) the generalized IoU loss and \(\hat{\sigma}\) the optimal assignment computed with the Hungarian algorithm.
\[\cal{L}_{box}(b_{i}, \hat{b}_{\hat{\sigma}}(i)) = \lambda_{\rm iou}\cal{L}_{iou}(b_{i}, \hat{b}_{\sigma(i)}) + \lambda_{\rm L1}||b_{i}- \hat{b}_{\sigma(i)}||_1 \]
with \(\cal{L}_{iou}\) the generalized IoU loss and \(\hat{\sigma}\) the optimal assignment computed with the Hungarian algorithm.
How does DETR produce N predictions.
The predictions come from the transformer decoder.
The decoder follows the standard architecture of the transformer, transforming \(N\) embeddings of size \(d\) using multi-headed self- and encoder-decoder attention mechanisms. The difference with the original transformer is that our model decodes the \(N\) objects in parallel at each decoder layer.
Since the decoder is also permutation-invariant, the \(N\) input embeddings must be different to produce different results. These input embeddings are learnt positional encodings that we refer to as object queries, and similarly to the encoder, we add them to the input of each attention layer.
The \(N\) object queries are transformed into an output embedding by the decoder. They are then independently decoded into box coordinates and class labels by a feed forward network, resulting \(N\) final predictions. Using self- and encoder-decoder attention over these embeddings, the model globally reasons about all objects together using pair-wise relations between them, while being able to use the whole image as context.
How many FLOPS and parameters does the DETR model have? And how accurate is it on COCO?
86G FLOPS and 41M parameters with AP 42.0 on COCO.