Give an overview of the Latent Diffusion Model (Stable Diffusion architecture).
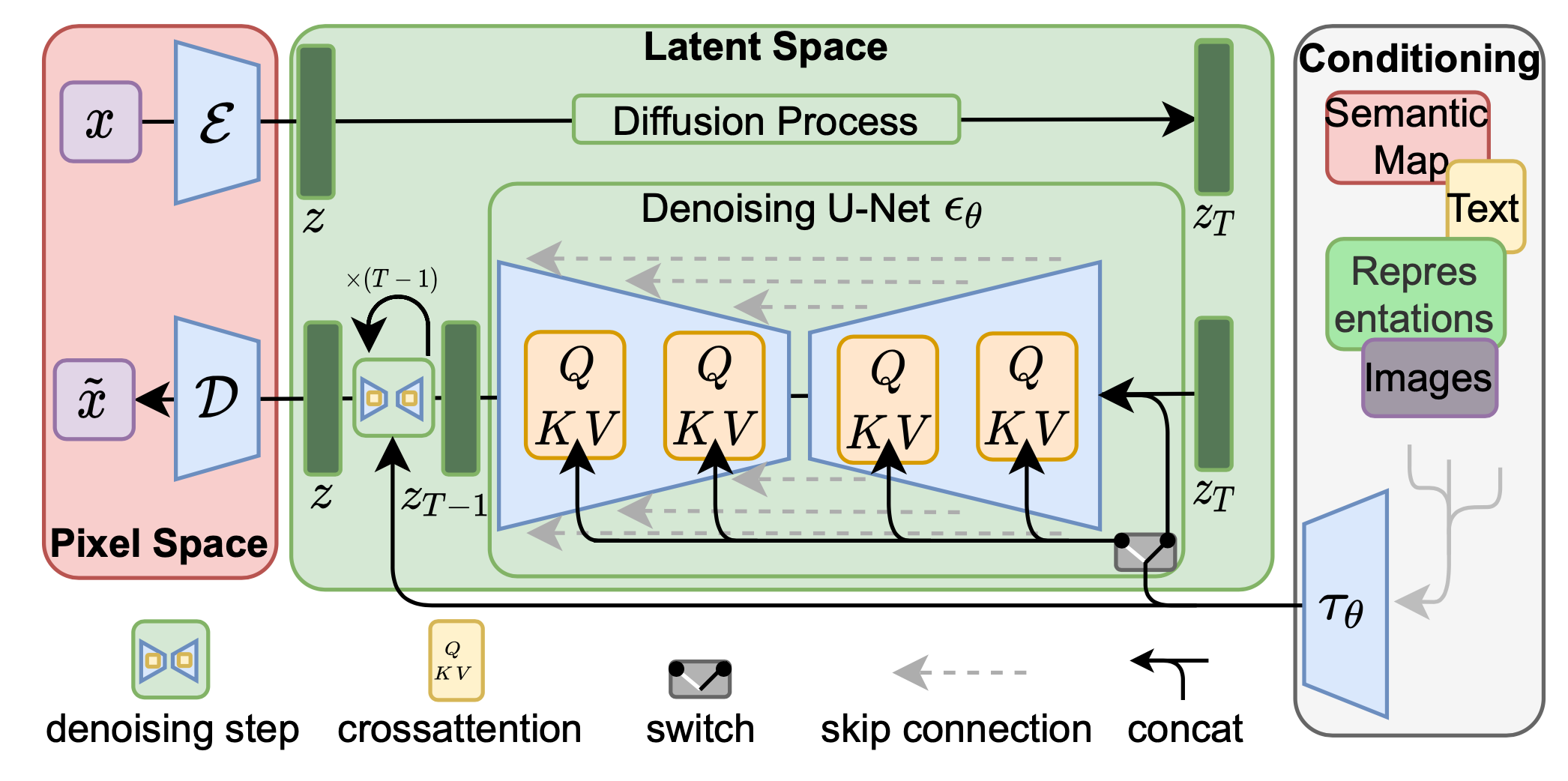
An encoder \(\mathcal{E}\) is used to compress the input image \(\mathbf{x} \in \mathbb{R}^{H \times W \times 3}\) to a smaller 2D latent vector \(\mathbf{z} = \mathcal{E}(\mathbf{x}) \in \mathbb{R}^{h \times w \times c}\), where the downsampling rate \(f=H/h=W/w=2^m, m \in \mathbb{N}\). A decoder \(\mathcal{D}\) reconstructs the images from the latent vector: \(\tilde{\mathbf{x}} = \mathcal{D}(\mathbf{z})\).
The diffusion and denoising processes happen on the latent vector \(\mathbf{z}\).
The denoising model is a time-conditioned U-Net, augmented with the cross-attention mechanism to handle flexible conditioning information for image generation.
To process \(y\) from various modalities, a domain specific encoder \(\tau_\theta\) that projects \(y\) to an intermediate representation \(\tau_\theta(y) \in \mathbb{R}^{M \times d_\tau}\) is used.
\[\begin{aligned} &\text{Attention}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = \text{softmax}\Big(\frac{\mathbf{Q}\mathbf{K}^\top}{\sqrt{d}}\Big) \cdot \mathbf{V} \\ &\text{where }\mathbf{Q} = \mathbf{W}^{(i)}_Q \cdot \varphi_i(\mathbf{z}_i),\; \mathbf{K} = \mathbf{W}^{(i)}_K \cdot \tau_\theta(y),\; \mathbf{V} = \mathbf{W}^{(i)}_V \cdot \tau_\theta(y) \\ &\text{and } \mathbf{W}^{(i)}_Q \in \mathbb{R}^{d \times d^i_\epsilon},\; \mathbf{W}^{(i)}_K, \mathbf{W}^{(i)}_V \in \mathbb{R}^{d \times d_\tau},\; \varphi_i(\mathbf{z}_i) \in \mathbb{R}^{N \times d^i_\epsilon},\; \tau_\theta(y) \in \mathbb{R}^{M \times d_\tau} \end{aligned}\]Where \(\varphi(\mathbf{z}_i) \in \mathbb{R}^{N \times d_\epsilon^i}\) denotes a (flattened) intermediate representation of the UNet implementation \(\epsilon_\theta\).
How is the latent diffusion model trained?
The compression part (e.g. encoder \(\mathcal{E}\) and decoder \(\mathcal{D}\)) and diffusion part are trained in different phases (first compression then diffusion).
Usually the compression part is taken from a pretrained network such as CLIP.
How does the latent diffusion model avoid arbitratily high-variance latent spaces?
It proposes two variants to deal with this:
- KL-reg: a small Kullback-Leibler penalty is imposed towards a standard normal distribution over the learned latent, similar to a VAE.
- VQ-reg: a vector quantization layer is used within the decoder, similar to VQVAE but the quantization layer is absorbed by the decoder.