What does NeRF stand for?
Neural Radiance Fields
What is the NeRF algorithm used for?
NeRF represents a 3D scene with a deep neural network, whose input is a single continuous 5D coordinate (spatial location (\(x, y, z\)) and viewing direction (\(\theta, \phi\))) and whose output is the volume density \(\sigma\) and view-dependent RGB color at that location.
Give an overview of the NeRF scene representation and rendering procedure:
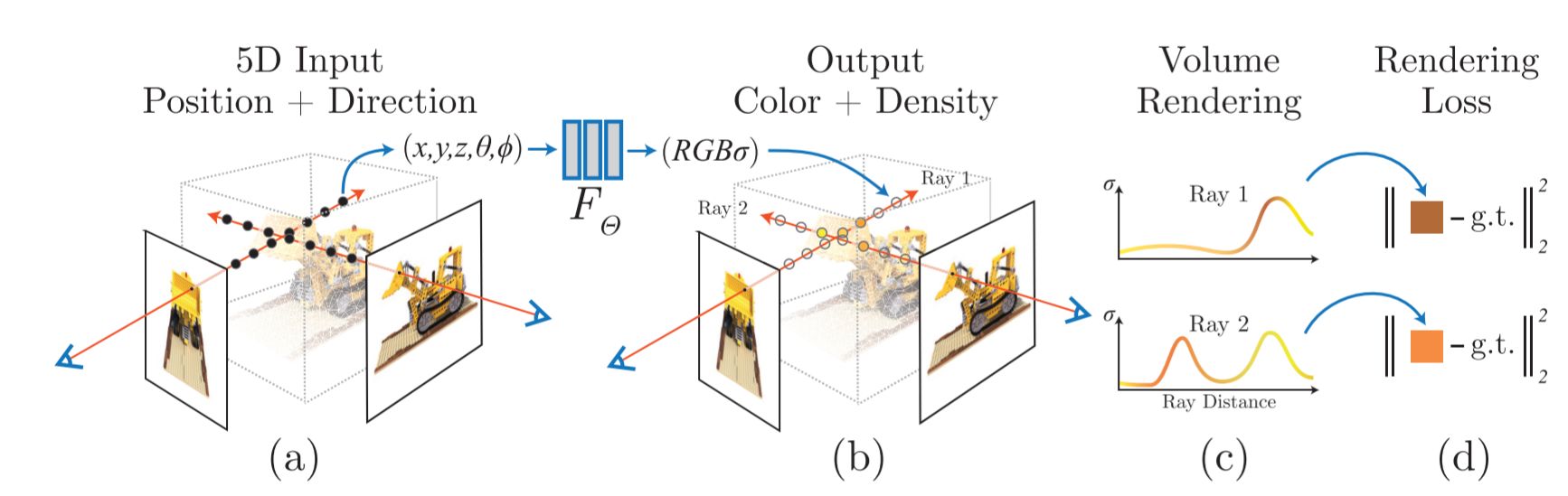
Synthesize images by sampling 5D coordinates (location and viewing direction) along camera rays (a), feed those locations into an MLP to produce a color and volume density (b), and use volume rendering techniques to composite these values into an image (c). This rendering function is differentiable, so you can optimize the scene representation by minimizing the residual between synthesized and ground truth observed images (d).
How do you go from input images to training data in NeRF?
For each image in the train set a camera pose matrix is given from which an origin position \((x,y,z)\) in world coordinates and a view direction \(\mathbf{d} \in \mathbb{R}^3\) can be derived.
The origin is the same for every pixel in the same image.
The origin is the same for every pixel in the same image.
In the paper the view direction is characterized by two angles \(\theta, \phi\) however in most implementations (including the official one) this is characterized by a 3D vector.
How is the neural network in NeRF representing \(F_\Theta : (\mathbf{x},\mathbf{d}) \rightarrow (\mathbf{c},\sigma)\) implemented?
To encourage the representation to be multiview consistent the network is restricted to predict the volume density \(\sigma\) as a function of only the location \(x\), while allowing the RGB color \(\mathbf{c}\) to be predicted as a function of both location and viewing direction.
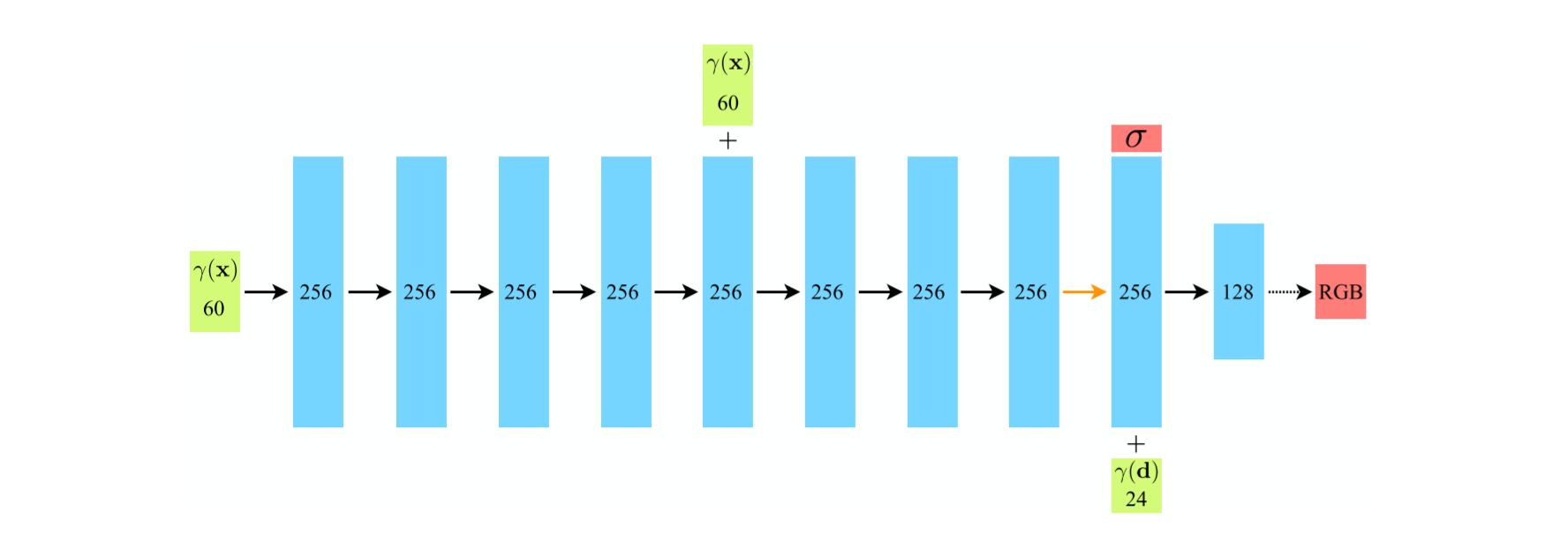
Input vectors are shown in green, intermediate hidden layers are shown in blue, output vectors are shown in red, and the number inside each block signifies the vector’s dimension. All layers are standard fully-connected layers, black arrows indicate layers with ReLU activations, orange arrows indicate layers with no activation, dashed black arrows indicate layers with sigmoid activation, and \(+\) denotes vector concatenation. The positional encoding of the input location \((\gamma(\mathbf{x}))\) is passed through 8 fully-connected ReLU layers, each with 256 channels. It follows the DeepSDF architecture and includes a skip connection that concatenates this input to the fifth layer’s activation. An additional layer outputs the volume density \(\sigma\) (which is rectified using a ReLU to ensure that the output volume density is nonnegative) and a 256-dimensional feature vector. This feature vector is concatenated with the positional encoding of the input viewing direction \((\gamma(\mathbf{d}))\), and is processed by an additional fully-connected ReLU layer with 128 channels. A final layer (with a sigmoid activation) outputs the emitted RGB radiance at position \(\mathbf{x}\), as viewed by a ray with direction \(\mathbf{d}\).

Input vectors are shown in green, intermediate hidden layers are shown in blue, output vectors are shown in red, and the number inside each block signifies the vector’s dimension. All layers are standard fully-connected layers, black arrows indicate layers with ReLU activations, orange arrows indicate layers with no activation, dashed black arrows indicate layers with sigmoid activation, and \(+\) denotes vector concatenation. The positional encoding of the input location \((\gamma(\mathbf{x}))\) is passed through 8 fully-connected ReLU layers, each with 256 channels. It follows the DeepSDF architecture and includes a skip connection that concatenates this input to the fifth layer’s activation. An additional layer outputs the volume density \(\sigma\) (which is rectified using a ReLU to ensure that the output volume density is nonnegative) and a 256-dimensional feature vector. This feature vector is concatenated with the positional encoding of the input viewing direction \((\gamma(\mathbf{d}))\), and is processed by an additional fully-connected ReLU layer with 128 channels. A final layer (with a sigmoid activation) outputs the emitted RGB radiance at position \(\mathbf{x}\), as viewed by a ray with direction \(\mathbf{d}\).
What trick is needed in NeRF to make the network work on inputs \((x,y,z,\theta,\phi)\)?
Each of these inputs is projected to a higher dimension using positional encodings.
\(\gamma(p) = (\sin(2^0\pi p), \cos(2^0\pi p), ..., \sin(2^{L-1}\pi p), \cos(2^{L-1}\pi p)\)
\(\gamma(p) = (\sin(2^0\pi p), \cos(2^0\pi p), ..., \sin(2^{L-1}\pi p), \cos(2^{L-1}\pi p)\)
In volume rendering, how do you go from a volume density \(\sigma(\mathbf{x})\) and a color \(\mathbf{c}(\mathbf{x})\) to a color \(C(\mathbf{r})\) of a camera ray \(\mathbf{r}(t) = \mathbf{o} + t \mathbf{d}\) with near and far bounds \(t_n, t_f\)?
\[C(\mathbf{r}) = \int_{t_n}^{t_f}T(t)\sigma(\mathbf{r}(t))\mathbf{c}(\mathbf{r}(t),\mathbf{d})dt\,, \textrm{ where }T(t) = \operatorname{exp}({-\int_{t_n}^{t}\sigma(\mathbf{r}(s))ds})\,.\]The function \(T(t)\) denotes the accumulated transmittance along the ray from \(t_n\) to \(t\), i.e. the probability that the ray travels from \(t_n\) to \(t\) without hitting any other particle.
This integral \(C(\mathbf{r})\) gets numerically estimated using quadrature. (see paper for details)
In NeRF, what is the formula for \(\hat{C}(\mathbf{r})\) , the estimated version of \(C(\mathbf{r})\)?
\[\hat{C}(\mathbf{r})=\sum_{i=1}^{N}T_i (1-\operatorname{exp}({-\sigma_i \delta_i}) )\mathbf{c}_i, \textrm{ where }
T_i=\operatorname{exp}({- \sum_{j=1}^{i-1} \sigma_j \delta_j})\]and where \(\delta_i = t_{i+1} - t_i\) is the distance between adjacent samples.