Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity
Give an overview of the Switch Transformer.
The Switch Transformer is transformer based model that incorporates a Mixture of Experts (MoE) in the feed forward layers.
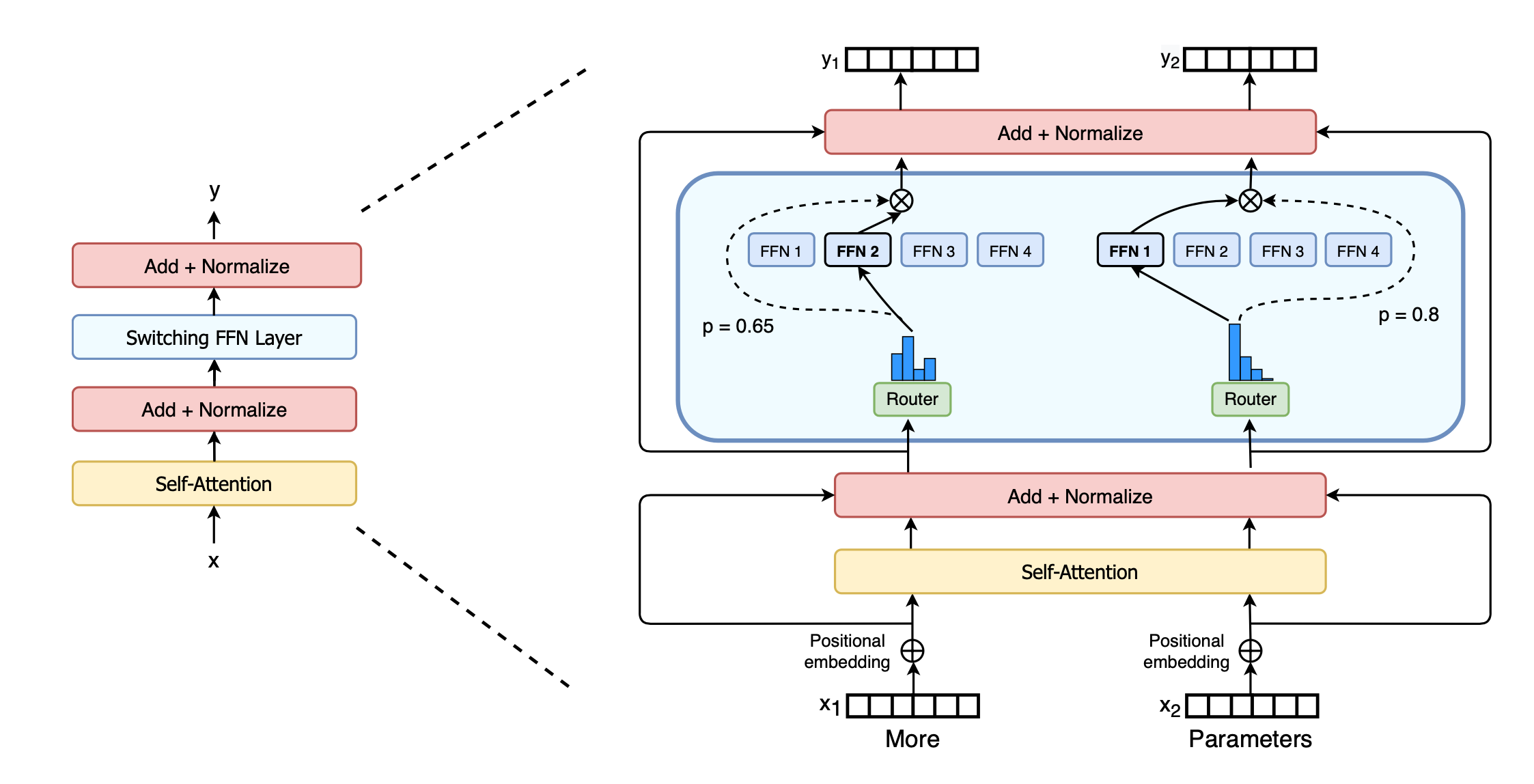
The Switch Transformer encoder block replaces the dense feed forward network FFN with a sparse Switch FFN layer.
The layer operates independently on the tokens in the sequence.
The Switch FFN layer returns the output of the selected FFN multiplied by the router gate value (dotted-line).

The Switch Transformer encoder block replaces the dense feed forward network FFN with a sparse Switch FFN layer.
The layer operates independently on the tokens in the sequence.
The Switch FFN layer returns the output of the selected FFN multiplied by the router gate value (dotted-line).
How is routing/gating done in the Switch Transformer MoE?
The Switch Transformer uses the same gating network as introduced in the original MoE paper of Shazeer et al. 2017 but it only routes to 1 expert.
So \(k = 1\).
So for the Switch FFN: \(y = p_i(x)E_i(x)\) where \(i = \operatorname{argmax}(p(x))\).
So \(k = 1\).
So for the Switch FFN: \(y = p_i(x)E_i(x)\) where \(i = \operatorname{argmax}(p(x))\).
How is the load/importance balanced in the Switch Transformer?
Just like the MoE paper from Shazeer et al. 2017 they use an auxiliarly loss.
The auxiliary loss in the Switch Transformer combines load-balancing and importance-weighting (this were two seperate losses in Shazeer et al.).
Given \(N\) experts indexed by \(i\) and a batched input \(X\) with \(T\) tokens in total, the auxiliary loss is computed as the scaled dot-product between vectors \(f_i\) and \(P_i\),
\[\mathcal{L} = \alpha \cdot N \cdot \sum_{i=1}^N f_i \cdot P_i\]
where \(f_i\) is the fraction of tokens dispatch to expert \(i\),
\[f_i = \frac{1}{T}\sum_{x \in X}\mathbb{1}\{\operatorname{argmax}(p(x))=i\}\]and \(P_i\) is the fraction of the router probability allocated for expert \(i\),
\[P_i = \frac{1}{T}\sum_{x \in X} p_i(x)\]
This loss miminizes under a uniform distribution of \(P\) and \(f\).
The auxiliary loss in the Switch Transformer combines load-balancing and importance-weighting (this were two seperate losses in Shazeer et al.).
Given \(N\) experts indexed by \(i\) and a batched input \(X\) with \(T\) tokens in total, the auxiliary loss is computed as the scaled dot-product between vectors \(f_i\) and \(P_i\),
\[\mathcal{L} = \alpha \cdot N \cdot \sum_{i=1}^N f_i \cdot P_i\]
where \(f_i\) is the fraction of tokens dispatch to expert \(i\),
\[f_i = \frac{1}{T}\sum_{x \in X}\mathbb{1}\{\operatorname{argmax}(p(x))=i\}\]and \(P_i\) is the fraction of the router probability allocated for expert \(i\),
\[P_i = \frac{1}{T}\sum_{x \in X} p_i(x)\]
This loss miminizes under a uniform distribution of \(P\) and \(f\).
What is the capacity factor mentioned in Switch Transformer?
For implementation/efficiency reasons, the tensor shapes of each expert is fixed ahead of time.
The expert capacity, which is the number of tokens each expert computes, is set by evenly dividing the number of tokens in the batch across the number of experts, and then further expanding it by the capacity factor.
\[\text{expert capacity }=(\frac{\text{tokens per batch}}{\text{number of experts}}) \times \text{ capacity factor}\]A capacity factor great than 1.0 creates additional buffer to accomodate for when tokens are not perfectly balanced across experts.
The expert capacity, which is the number of tokens each expert computes, is set by evenly dividing the number of tokens in the batch across the number of experts, and then further expanding it by the capacity factor.
\[\text{expert capacity }=(\frac{\text{tokens per batch}}{\text{number of experts}}) \times \text{ capacity factor}\]A capacity factor great than 1.0 creates additional buffer to accomodate for when tokens are not perfectly balanced across experts.
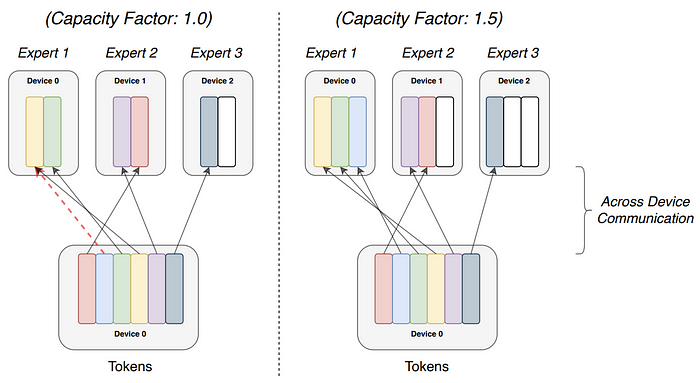
What happens when more tokens are assigned to an expert than there is capacity for, in the Switch Transformer?
If too many tokens are routed to an expert, computation is skipped and the token representation is passed directly to the next layer through the residual.