What is the loss used in Barlow Twins?
\[\begin{aligned}
\mathcal{L}_\text{BT} &= \underbrace{\sum_i (1-\mathcal{C}_{ii})^2}_\text{invariance term} + \lambda \underbrace{\sum_i\sum_{i\neq j} \mathcal{C}_{ij}^2}_\text{redundancy reduction term} \\ \text{where } \mathcal{C}_{ij} &= \frac{\sum_b \mathbf{z}^A_{b,i} \mathbf{z}^B_{b,j}}{\sqrt{\sum_b (\mathbf{z}^A_{b,i})^2}\sqrt{\sum_b (\mathbf{z}^B_{b,j})^2}}
\end{aligned}\]and \(\mathbf{z}\) are the embeddings of the networks and \(\lambda\) a positive constant trading off the importance of both terms of the loss.
Intuitively, the invariance term of the objective, by trying to equate the diagonal elements of the cross-correlation matrix to 1, makes the embedding invariant to the distortions applied.
The redundancy reduction term, by trying to equate the off-diagonal elements of the cross-correlation matrix to 0, decorrelates the different vector components of the embedding. This decorrelation reduces the redundancy between output units, so that the output units contain non-redundant information about the sample.
The redundancy reduction term, by trying to equate the off-diagonal elements of the cross-correlation matrix to 0, decorrelates the different vector components of the embedding. This decorrelation reduces the redundancy between output units, so that the output units contain non-redundant information about the sample.
Give an overview of the Barlow Twins method.
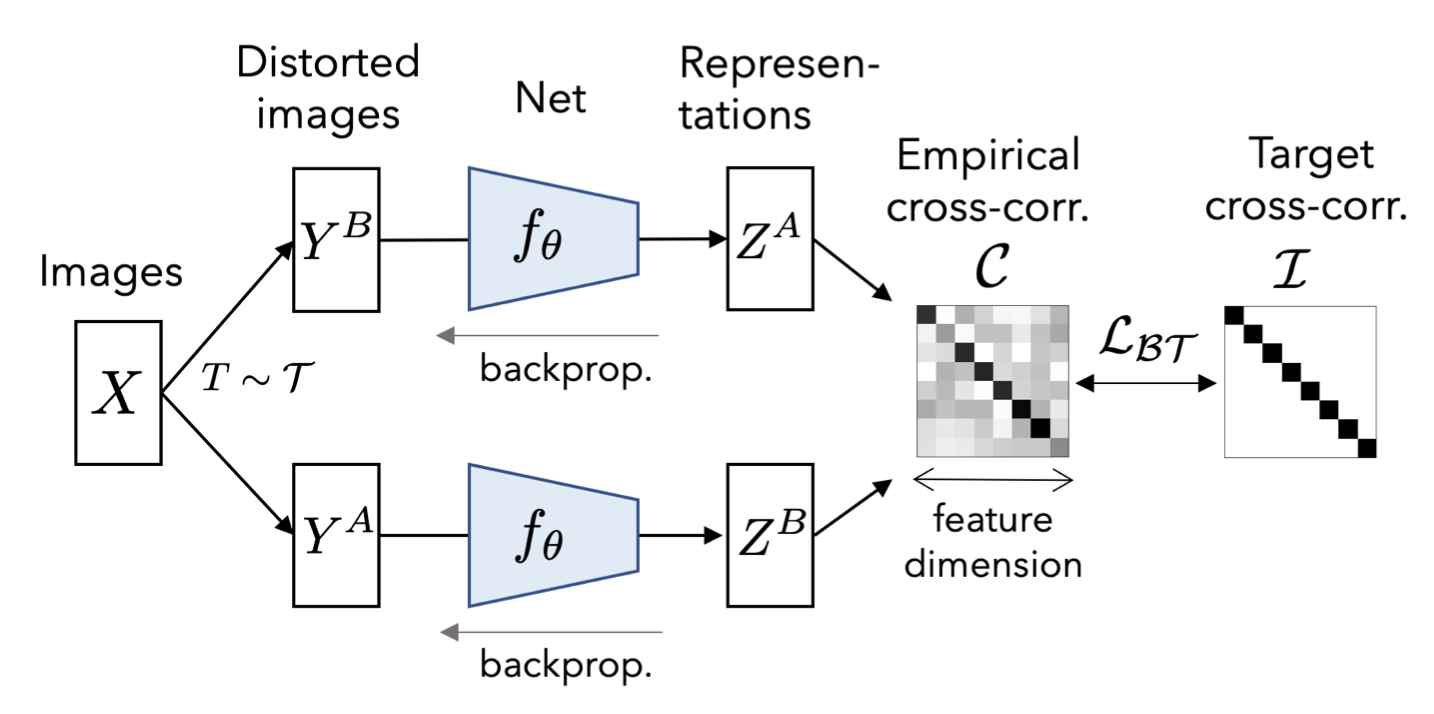
Barlow Twins's objective function measures the cross-correlation matrix between the embeddings of two identical networks fed with distorted versions of a batch of samples, and tries to make this matrix close to the identity. This causes the embedding vectors of distorted versions of a sample to be similar, while minimizing the redundancy between the components of these vectors.
Give PyTorch-style pseudocode for Barlow Twins.

What is an important advantage of Barlow Twins compared to previous work?
It does not require large number of negative samples and can thus operate on small batches.