Give schematic of the contrastive learning framework used in SimCLR.
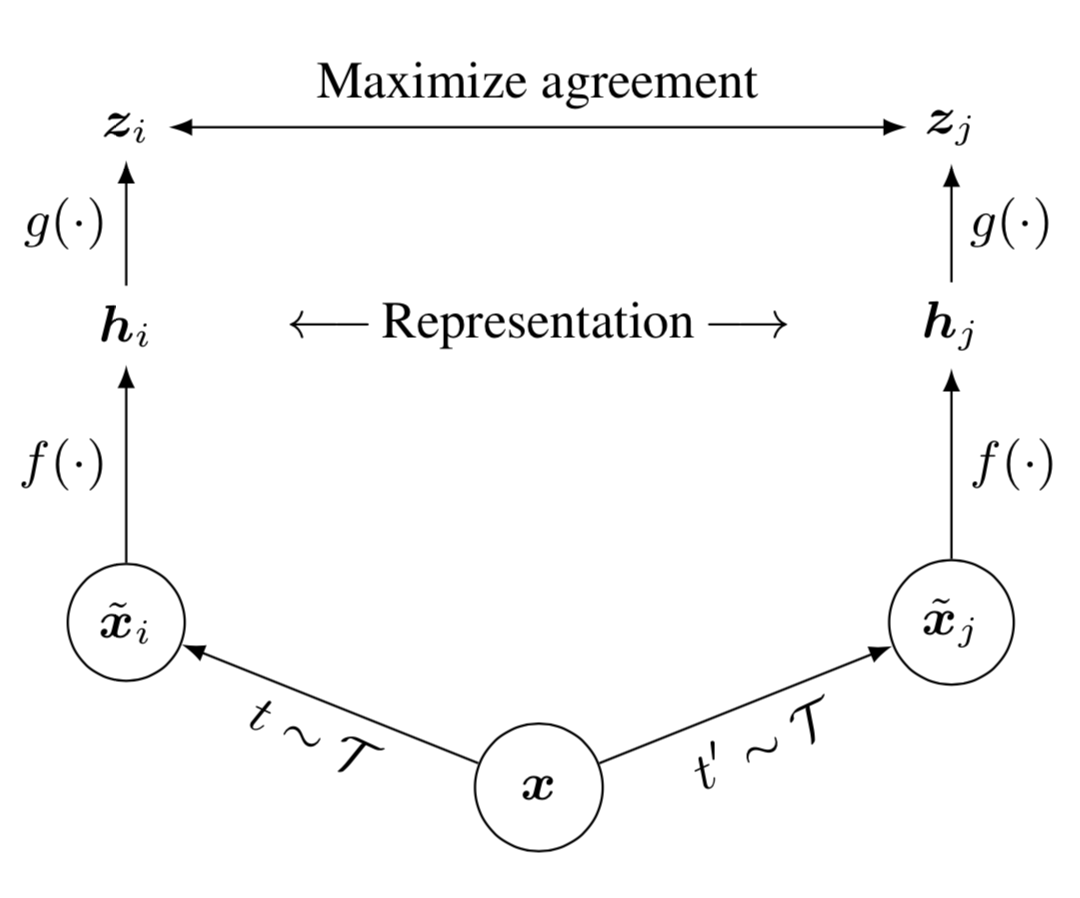
Framework for contrastive learning of visual representations.
Two separate data augmentations operators are sampled from the same family of augmentations (\(t, t' \sim \mathcal{T}\)) and applied to each data example to obtain two correlated views. A base encoder network \(f(.)\) and a projection head \(g(.)\) are trained to maximize agreement using a contrastive loss. After training is completed, throw away the projection head \(g(.)\) and use encoder \(f(.)\) and representation \(\mathbf{h}\) for downstream tasks.
Two separate data augmentations operators are sampled from the same family of augmentations (\(t, t' \sim \mathcal{T}\)) and applied to each data example to obtain two correlated views. A base encoder network \(f(.)\) and a projection head \(g(.)\) are trained to maximize agreement using a contrastive loss. After training is completed, throw away the projection head \(g(.)\) and use encoder \(f(.)\) and representation \(\mathbf{h}\) for downstream tasks.
Which similarity metric is used in SimCLR?
Cosine similarity
This can be represented by using a dot product and scaling by the magnitudes.
\[s(\mathbf{u}, \mathbf{v}) = \frac{\mathbf{u}^T\mathbf{v}}{\|u\| \|v\|}\]
This can be represented by using a dot product and scaling by the magnitudes.
\[s(\mathbf{u}, \mathbf{v}) = \frac{\mathbf{u}^T\mathbf{v}}{\|u\| \|v\|}\]
Which loss function is used in SimCLR?
The loss function for a positive pair of examples \((i, j)\) is defined as:
\[\begin{aligned} \mathcal{L}_\text{SimCLR}^{(i,j)} &= - \log\frac{\exp(s(\mathbf{z}_i, \mathbf{z}_j) / \tau)}{\sum_{k=1}^{2N} \mathbb{1}_{[k \neq i]} \exp(s(\mathbf{z}_i, \mathbf{z}_k) / \tau)} \end{aligned}\]where \(s(.)\) is the similarity metric (usually cosine similarity).
The final loss is computed across all positive pairs, both \((i,j)\) and \((j,i)\).
\[\begin{aligned} \mathcal{L}_\text{SimCLR}^{(i,j)} &= - \log\frac{\exp(s(\mathbf{z}_i, \mathbf{z}_j) / \tau)}{\sum_{k=1}^{2N} \mathbb{1}_{[k \neq i]} \exp(s(\mathbf{z}_i, \mathbf{z}_k) / \tau)} \end{aligned}\]where \(s(.)\) is the similarity metric (usually cosine similarity).
The final loss is computed across all positive pairs, both \((i,j)\) and \((j,i)\).
This loss can be called the normalized temperature-scaled cross entropy loss (NT-Xent).
It has been used in prior work.
It has been used in prior work.
Give the training algorithm for SimCLR.
input: batch size \(N\), temperature constant \(\tau\), encoder \(f\), projection head \(g\), augmentation family \(\mathcal{T}\).
for sampled minibatch \(\{\mathbf{x}_k\}^N_{k=1}\) do:
for all \(k \in \{1, \dots, N\}\) do:
sample two augmentation functions \(t \sim \mathcal{T}\), \(t' \sim \mathcal{T}\)
\(\tilde{\mathbf{x}}_{2k - 1}= t(\mathbf{x}_k)\)
\(\tilde{\mathbf{x}}_{2k}= t'(\mathbf{x}_k)\)
\(\mathbf{h}_{2k - 1}= f(\tilde{\mathbf{x}}_{2k -1 })\)
\(\mathbf{h}_{2k}= f(\tilde{\mathbf{x}}_{2k})\)
\(\mathbf{z}_{2k-1} = g(\mathbf{h}_{2k-1})\)
\(\mathbf{z}_{2k} = g(\mathbf{h}_{2k})\)
for all \(i \in \{1, \dots, 2N\}\) and \(j \in \{1, \dots, 2N\}\) do:
\(s_{i,j} = \frac{\mathbf{z}_i^\top\mathbf{z}_j}{\|\mathbf{z}_i\| \|\mathbf{z}_j\|}\)
define \(\mathcal{L}^{(i,j)} = - \log\frac{\exp(s_{i,j} / \tau)}{\sum_{k=1}^{2N} \mathbb{1}_{[k \neq i]} \exp(s_{i,k} / \tau)}\)
\(\mathcal{L} = \frac{1}{2N} \sum^N_{k=1}[\mathcal{L}^{(2k-1,2k)} +\mathcal{L}^{(2k,2k-1)}]\)
update networks \(f\) and \(g\) to minimize \(\mathcal{L}\)
return encoder \(f\) and throw away \(g\)
for sampled minibatch \(\{\mathbf{x}_k\}^N_{k=1}\) do:
for all \(k \in \{1, \dots, N\}\) do:
sample two augmentation functions \(t \sim \mathcal{T}\), \(t' \sim \mathcal{T}\)
\(\tilde{\mathbf{x}}_{2k - 1}= t(\mathbf{x}_k)\)
\(\tilde{\mathbf{x}}_{2k}= t'(\mathbf{x}_k)\)
\(\mathbf{h}_{2k - 1}= f(\tilde{\mathbf{x}}_{2k -1 })\)
\(\mathbf{h}_{2k}= f(\tilde{\mathbf{x}}_{2k})\)
\(\mathbf{z}_{2k-1} = g(\mathbf{h}_{2k-1})\)
\(\mathbf{z}_{2k} = g(\mathbf{h}_{2k})\)
for all \(i \in \{1, \dots, 2N\}\) and \(j \in \{1, \dots, 2N\}\) do:
\(s_{i,j} = \frac{\mathbf{z}_i^\top\mathbf{z}_j}{\|\mathbf{z}_i\| \|\mathbf{z}_j\|}\)
define \(\mathcal{L}^{(i,j)} = - \log\frac{\exp(s_{i,j} / \tau)}{\sum_{k=1}^{2N} \mathbb{1}_{[k \neq i]} \exp(s_{i,k} / \tau)}\)
\(\mathcal{L} = \frac{1}{2N} \sum^N_{k=1}[\mathcal{L}^{(2k-1,2k)} +\mathcal{L}^{(2k,2k-1)}]\)
update networks \(f\) and \(g\) to minimize \(\mathcal{L}\)
return encoder \(f\) and throw away \(g\)
In contrastive frameworks such as SimCLR, why is the similarity optimized on a separate projection head \(g\)?
It likely due to the fact that the contrastive representation needs to be invariant to many data transformations, as such information such as color is removed in this representation while this may be useful for downstream tasks. By adding an additional projection head, \(g\) can remove information that may be useful for downstream tasks but needs to be removed in order to maximize the contrastive similarity.However all of this is found empirically.