SSD: Single Shot MultiBox Detector
What is the general architecture of the Single-Short Detector (SSD)?
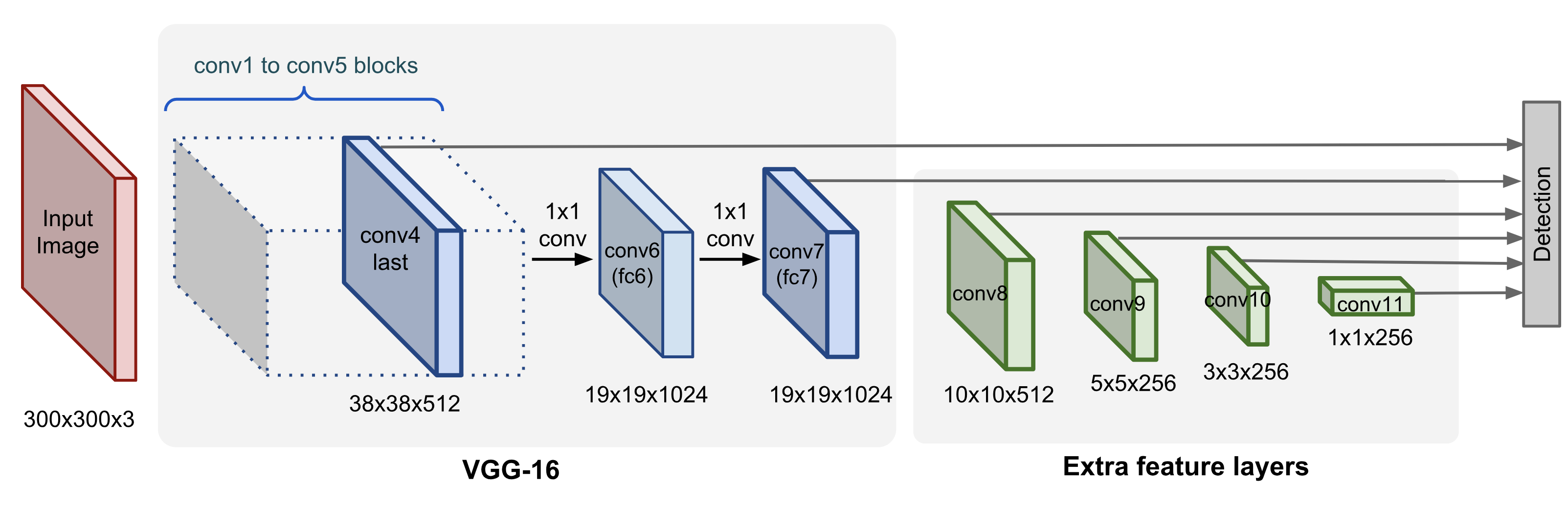
A Single-Shot Detector uses a backbone network, to which it adds additional convolutional feature layers.
These layers decrease in size progressively and allow predictions at multiple scales.
Attached to each feature layer (or optionally an exisiting feaure layer from the base network) is a convolutional detection layer that produces a fixed set of predictions.
These predicted bounding boxes and scores are then processed by a non-maximum suppression step to produce the final detections.
How does SSD produce predicted bounding boxes?
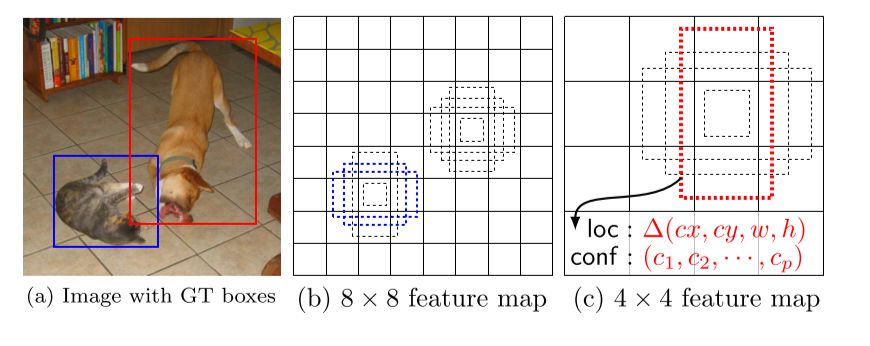
In a convolutional fashion, SSD evaluates a small set (e.g. 4) of default boxes of different aspect ratios at each location in several feature maps with different scales (e.g. \(8 \times 8\) and \(4 \times 4\) in (b) and (c)). For each default box, we predict
both the shape offsets and the confidences for all object categories (\((c_1, c_2,... , c_p)\)).
What are the defining parameters of anchor boxes in SSD?
Anchor boxes are defined by their scale \(s\) and aspect ratio \(a\).
The width and the height of the each default box is then computed as: \(w = s\sqrt{a}\), \(h = \frac{s}{\sqrt{a}}\).
The width and the height of the each default box is then computed as: \(w = s\sqrt{a}\), \(h = \frac{s}{\sqrt{a}}\).
Why are anchor boxes in SSD defined using the square root of the aspect ratio?
By taking the square root of the aspect ratio and multiplying it for one side and dividing for the other side, you still get the desired aspect ratio, while also keeping the area equal to the scale\(^{[1]}\).


[1]: https://twitter.com/Mxbonn/status/1252933371682066432
During training, how does SSD determine which default bounding boxes correspond to a ground truth box?
A default bounding box matches any ground truth box with jaccard overlap higher than a threshold (0.5).
This simplifies the learning problem, allowing the network to predict high scores for multiple overlapping default boxes rather than requiring it to pick only the one with maximum overlap.
During training, how does SSD deal with the large number of default bounding boxes that do not match with a ground truth box?
SSD uses a technique called hard negative mining:
Instead of using all the negative examples, SSD training sorts them using the highest confidence loss for each default box and picks the top ones so that the ratio between the negatives and positives is at most \(3:1\).
Instead of using all the negative examples, SSD training sorts them using the highest confidence loss for each default box and picks the top ones so that the ratio between the negatives and positives is at most \(3:1\).
What loss function is used in SSD?
The loss function is the sum of a localization loss and a classification loss.
\[\mathcal{L} = \frac{1}{N}(\mathcal{L}_\text{cls} + \alpha \mathcal{L}_\text{loc})\]
where \(N\) is the number of matched bounding boxes and \(\alpha\) balances the weights between two losses, picked by cross validation.
The localization loss is a smooth L1 loss between the predicted bounding box correction and the true values.
The classification loss is a softmax loss over multiple classes
\[\mathcal{L} = \frac{1}{N}(\mathcal{L}_\text{cls} + \alpha \mathcal{L}_\text{loc})\]
where \(N\) is the number of matched bounding boxes and \(\alpha\) balances the weights between two losses, picked by cross validation.
The localization loss is a smooth L1 loss between the predicted bounding box correction and the true values.
The classification loss is a softmax loss over multiple classes
How does SSD match predicted bounding boxes with the ground truth?
SSD matches each ground truth box to the default box with the best jaccard overlap and then matches default boxes to any ground truth with jaccard overlap higher than a threshold (0.5).
This simplifies the learning problem, allowing the network to predict high scores for multiple overlapping default boxes rather than requiring it to pick only the one with maximum overlap.