What is according to the RetinaNet paper the main obstacle for one-stage detectors to achieve state-of-the-art accuracy?
Class imbalance during training.
Note: More recent one-stage detectors have not adopted focal loss and have shown that it does not necessarily result in better accuracy.
How is class imbalance an issue for object detectors and how does SSD solve this issue compared to RetinaNet?
One-stage object detectors evaluate \(10^4-10^5\) candidate locations per image but only a few locations contain objects. This imbalance causes two problems:
(1) training is inefficient as most locations are easy negatives
(2) the easy negatives can overwhelm training and lead to degenerate models.
SSD solves this by hard negative mining.
RetinaNet uses Focal Loss that down-weights easy examples.
(1) training is inefficient as most locations are easy negatives
(2) the easy negatives can overwhelm training and lead to degenerate models.
SSD solves this by hard negative mining.
RetinaNet uses Focal Loss that down-weights easy examples.
Give the mathematical definition for the Focal Loss.
\[FL(p_t) = -(1 - p_t)^{\gamma} log(p_t)\]
with \(\gamma \ge 0\) a tunable focusing parameter and where
\[ p_t = \begin{cases} p & \text{if } y = 1 \\
1 - p & \text{if } y = 0 \end{cases} \]
with \(p \in [0,1]\) the model's estimated probability for the class with label \(y=1\)
with \(\gamma \ge 0\) a tunable focusing parameter and where
\[ p_t = \begin{cases} p & \text{if } y = 1 \\
1 - p & \text{if } y = 0 \end{cases} \]
with \(p \in [0,1]\) the model's estimated probability for the class with label \(y=1\)
In practice we use an \(\alpha\)-balanced variant of the focal loss:
\[FL(p_t) = -\alpha_t(1 - p_t)^{\gamma} log(p_t)\]
\[FL(p_t) = -\alpha_t(1 - p_t)^{\gamma} log(p_t)\]

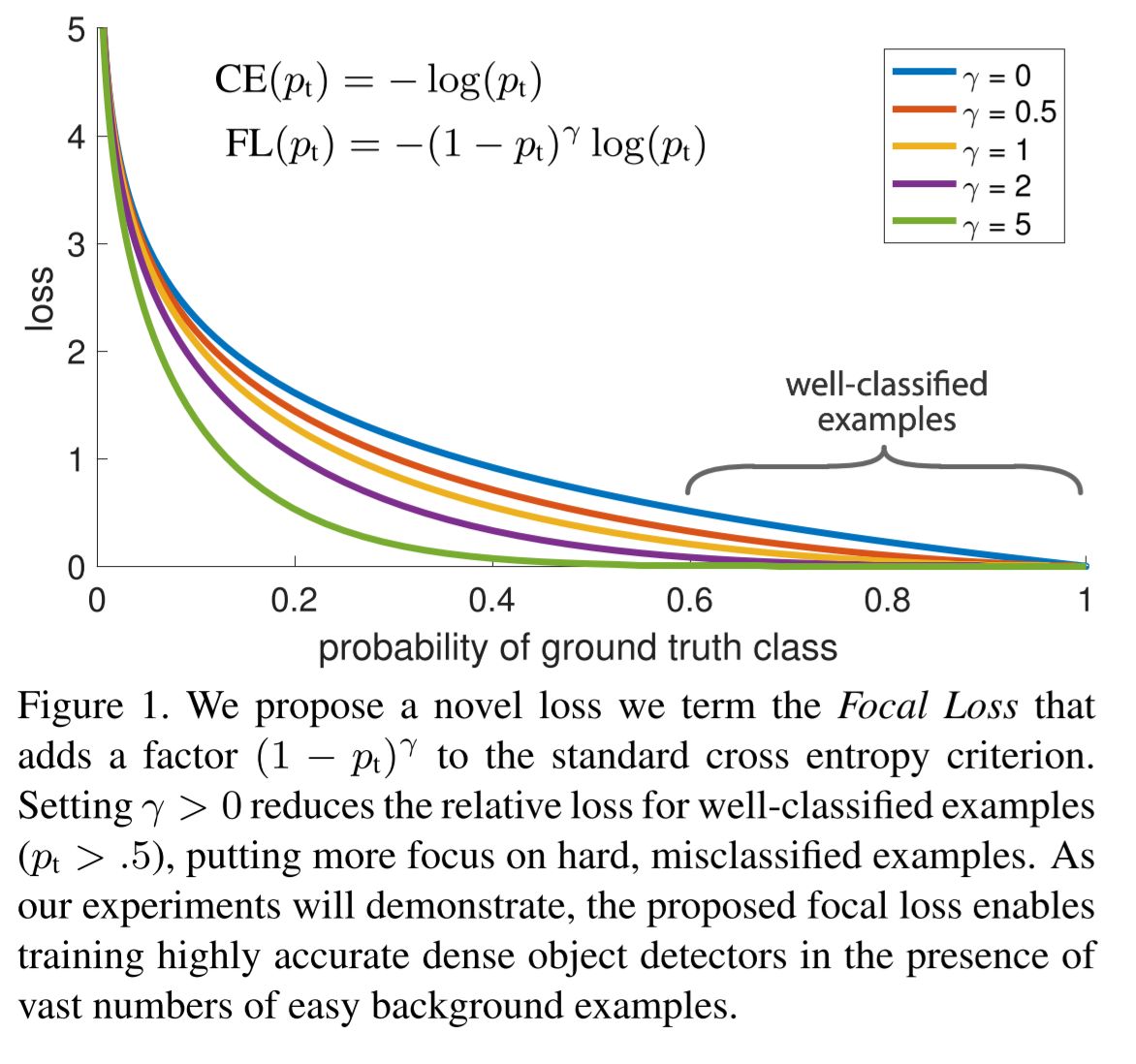
How does focal loss relate to the cross entropy loss?
Focal loss adds a modulating factor \((1 - p_t)\) to the cross entropy loss.
As \(p_t \to 1\), the factor goes to 0 and the loss for well-classified examples is down-weighted.
The focusing parameter \(\gamma\) smoothly adjusts the rate at which easy examples are downweighted. When \(\gamma = 0\), focal loss is equivalent to cross entropy loss, and as \(\gamma\) is increased the effect of the modulating factor is likewise increased.
As \(p_t \to 1\), the factor goes to 0 and the loss for well-classified examples is down-weighted.
The focusing parameter \(\gamma\) smoothly adjusts the rate at which easy examples are downweighted. When \(\gamma = 0\), focal loss is equivalent to cross entropy loss, and as \(\gamma\) is increased the effect of the modulating factor is likewise increased.

How is the focal loss of an entire image calculated?
The total focal loss of an image is computed as the sum of the focal loss over all anchors, normalized by the number of anchors assigned to a ground-truth box.
Draw the architecture of RetinaNet.
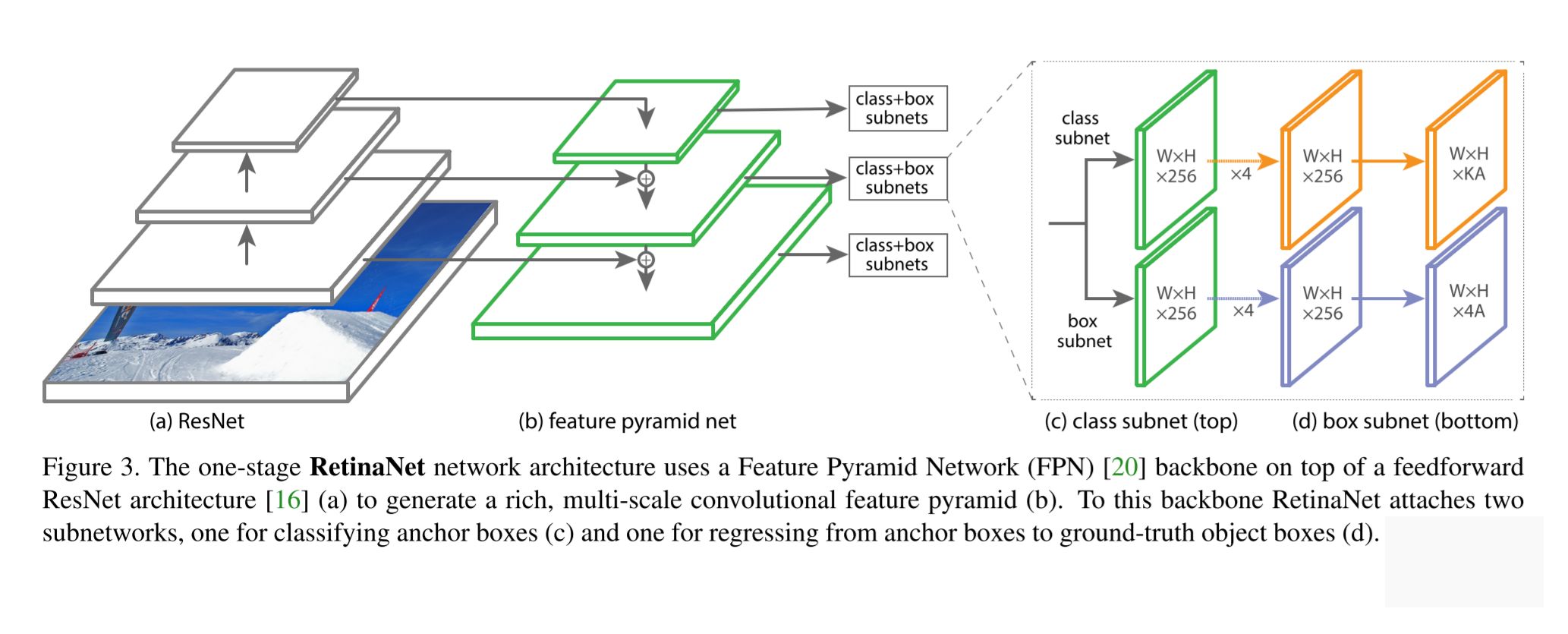
RetinaNet is a one-stage object detector with ResNet as backbone, a feature pyramid network (FPN) as neck and head that is shared for all feature layers.
RetinaNet follows the one-stage object detection architecture, the main innovation of RetinaNet was the loss function.