Proximal Policy Optimization Algorithms
What is Proximal Policy Optimization (PPO)?
Proximal Policy Optimization (PPO), is an algorithm that improves an agent’s training stability by avoiding too large policy updates. To do that, it uses a ratio that indicates the difference between the current and old policy and clips this ratio from a specific range \([1 - \epsilon, 1 + \epsilon]\).
Give the objective function used in Proximal Policy Optimization (PPO).
First, let’s denote the probability ratio between old and new policies as:
\[r_t(\theta) = \frac{\pi_\theta(a_t \vert s_t)}{\pi_{\theta_\text{old}}(a_t \vert s_t)}\]Then, the objective function of PPO becomes:
\[L^\text{PPO} (\theta) = \mathbb{E}_t [ r_t(\theta) \hat{A}_t]\]PPO imposes the constraint by forcing \(r_t(\theta)\) to stay within a small interval around 1, precisely \([1 - \epsilon, 1 + \epsilon]\), where \(\epsilon\) is a hyperparameter.
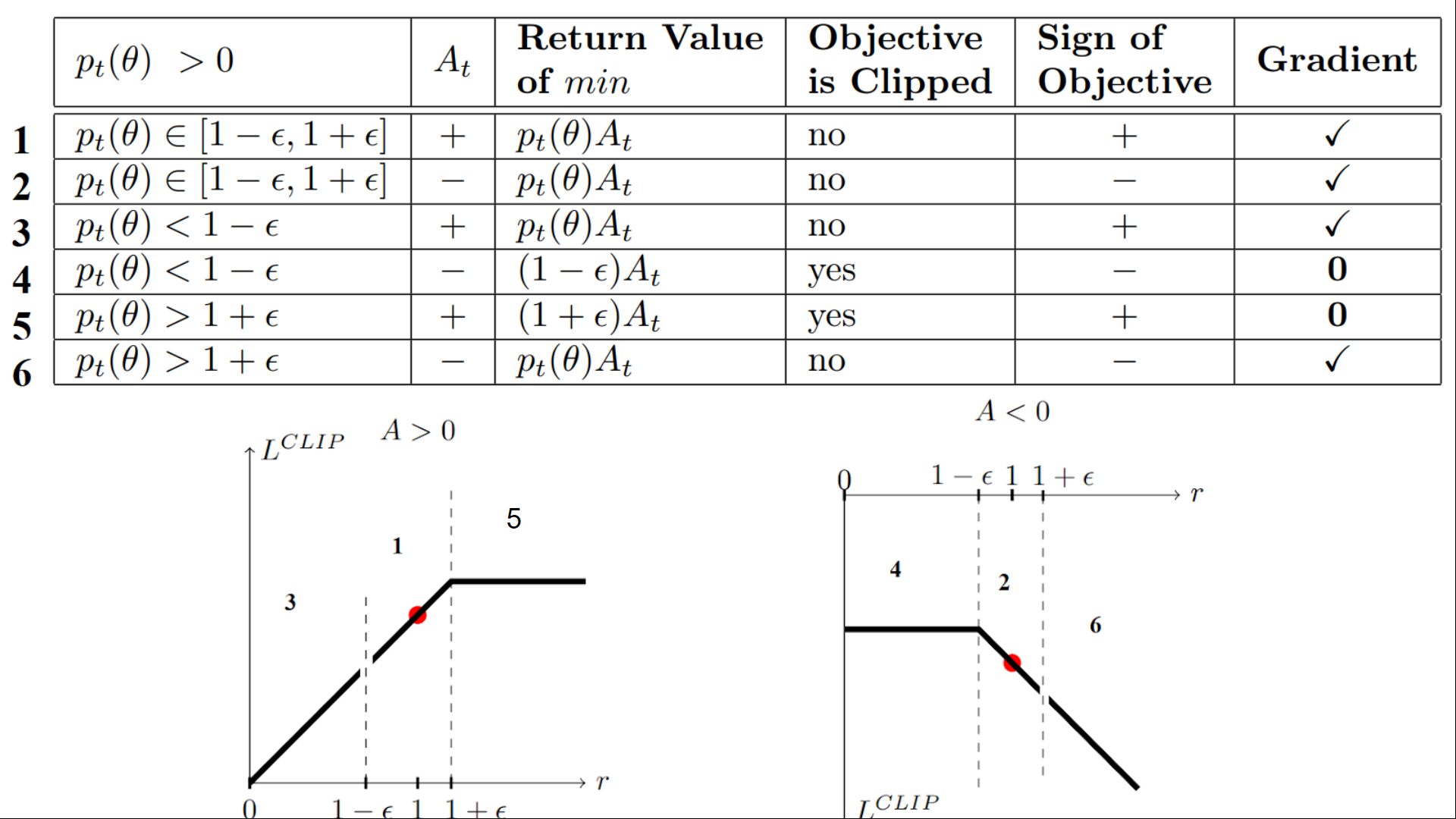
\[L^\text{CLIP} (\theta) = \mathbb{E}_t [ \min( r_t(\theta) \hat{A}_{t}, \text{clip}(r_t(\theta), 1 - \epsilon, 1 + \epsilon) \hat{A}_{t})]\]The objective function of PPO takes the minimum one between the original value and the clipped version and therefore we lose the motivation for increasing the policy update to extremes for better rewards.
When applying PPO on a network architecture with shared parameters for both policy (actor) and value (critic) functions, in addition to the clipped reward, the objective function is augmented with an error term on the value estimation (formula in red) and an entropy term (formula in blue) to encourage sufficient exploration.
\[L^\text{CLIP'} (\theta) = \mathbb{E}_t [ L^\text{CLIP} (\theta) - \color{red}{c_1 (V_\theta(s_t) - V_t^\text{target})^2} + \color{blue}{c_2 H(s_t, \pi_\theta(.))} ]\]
When applying PPO on a network architecture with shared parameters for both policy (actor) and value (critic) functions, in addition to the clipped reward, the objective function is augmented with an error term on the value estimation (formula in red) and an entropy term (formula in blue) to encourage sufficient exploration.
\[L^\text{CLIP'} (\theta) = \mathbb{E}_t [ L^\text{CLIP} (\theta) - \color{red}{c_1 (V_\theta(s_t) - V_t^\text{target})^2} + \color{blue}{c_2 H(s_t, \pi_\theta(.))} ]\]