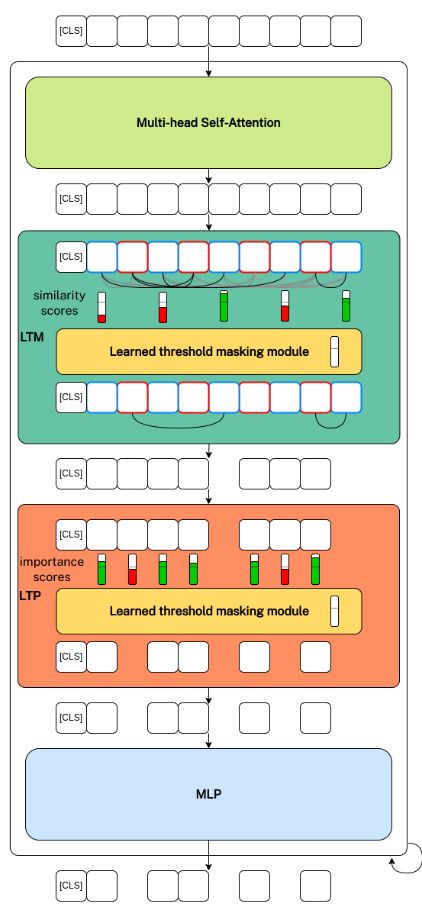
Learned Thresholds Token Merging and Pruning for Vision Transformers
How does LTMP combine token merging and token pruning?
LTMP adds learned threshold masking modules which learn a threshold for both pruning and merging. First token pairs that have a similarity score above the merging threshold are merged and then tokens with a importance score below the pruning threshold are pruned.
How many learnable parameters does LTMP introduce?
LTMP introduces only 2 learnable parameters per transformer block.
The learnable parameters are the thresholds, one for merging and one for pruning.
What loss function is used to train LTMP?
\[\mathcal{L} = \mathcal{L}_{CE} + \lambda(r_{target} - r_{FLOPs})^2\]
with \(r_{\text{FLOPs}} \approx{} \sum_{l=1}^L \frac{1}{L}\left(\frac{2\bar{\mathbf{m}}^{l-1}nd^2 + (\bar{\mathbf{m}}^{l-1}n)^2d + 4\bar{\mathbf{m}}^{l}nd^2}{6nd^2 + n^2d}\right)\) where they denote \(\phi_{\text{module}}(n,d)\) as a function that calculates the FLOPs of a module based on the number of tokens \(n\) and the embedding dimension \(d\).
\(\bar{\mathbf{m}}^l = \frac{1}{n}\sum_{i=1}^n \mathbf{m}^l_i\) is the percentage of input tokens that are kept after the $l$-th threshold masking operation and \(\bar{\mathbf{m}}^0 = 1\).
with \(r_{\text{FLOPs}} \approx{} \sum_{l=1}^L \frac{1}{L}\left(\frac{2\bar{\mathbf{m}}^{l-1}nd^2 + (\bar{\mathbf{m}}^{l-1}n)^2d + 4\bar{\mathbf{m}}^{l}nd^2}{6nd^2 + n^2d}\right)\) where they denote \(\phi_{\text{module}}(n,d)\) as a function that calculates the FLOPs of a module based on the number of tokens \(n\) and the embedding dimension \(d\).
\(\bar{\mathbf{m}}^l = \frac{1}{n}\sum_{i=1}^n \mathbf{m}^l_i\) is the percentage of input tokens that are kept after the $l$-th threshold masking operation and \(\bar{\mathbf{m}}^0 = 1\).
How do the learned threshold masks during LTMP mimic the effect of dropping tokens?
The attention function is modified such that it corresponds to attention as if it was only applied to the tokens that are not merged or pruned.
\[\operatorname{Attention\_with\_mask}(\mathbf{Q}, \mathbf{K}, \mathbf{V}, \mathbf{m}) = \mathbf{S}\mathbf{V}\]
where,
\[\mathbf{S}_{ij} = \frac{\exp(\mathbf{A}_{ij})\mathbf{m}_{j}}{\sum_{k=1}^N\exp(\mathbf{A}_{ik})\mathbf{m}_{k}}, 1\le i,j,k\le n\]
and,
\[\mathbf{A} = \mathbf{Q}\mathbf{K}^T/\sqrt{d_k} \in \mathbb{R}^{n\times n}\]
\[\operatorname{Attention\_with\_mask}(\mathbf{Q}, \mathbf{K}, \mathbf{V}, \mathbf{m}) = \mathbf{S}\mathbf{V}\]
where,
\[\mathbf{S}_{ij} = \frac{\exp(\mathbf{A}_{ij})\mathbf{m}_{j}}{\sum_{k=1}^N\exp(\mathbf{A}_{ik})\mathbf{m}_{k}}, 1\le i,j,k\le n\]
and,
\[\mathbf{A} = \mathbf{Q}\mathbf{K}^T/\sqrt{d_k} \in \mathbb{R}^{n\times n}\]
What does LTMP use as the importance score for pruning?
LTMP uses the mean column attention score \(s_i = \frac{1}{h \cdot n}\sum_{j=1}^h \sum_{k=1}^n S_{jki}\) which represents the attention \(x_i\) receives.
What does the threshold masking module in LTMP look like?
\[ M(\mathbf{s}^l_i, \theta^l) = \begin{cases}
1, &\text{if }\mathbf{s}^l_i > \theta^l\\
0, &\text{otherwise}
\end{cases}\]
where \(\theta\) is the learned threshold.
To make the threshold differentiable during backpropagation it is estimated using a straight-through estimator in the backward pass.
\( M(\mathbf{s}^l_i, \theta^l) = \sigma(\frac{\mathbf{s}^l_i - \theta^l}{\tau})\)
where \(\theta\) is the learned threshold.
To make the threshold differentiable during backpropagation it is estimated using a straight-through estimator in the backward pass.
\( M(\mathbf{s}^l_i, \theta^l) = \sigma(\frac{\mathbf{s}^l_i - \theta^l}{\tau})\)
Draw an overview of the LTMP framework.