Distilling the Knowledge in a Neural Network
What is Knowledge Distillation?
Knowledge distillation is model compression technique in which a small model is trained to mimic a pre-trained, larger model (or ensemble of models).
This training setting is sometimes referred to as teacher-student, where the large model is the teacher and the small model is the student.
This training setting is sometimes referred to as teacher-student, where the large model is the teacher and the small model is the student.
How do you train a network with knowledge distillation?
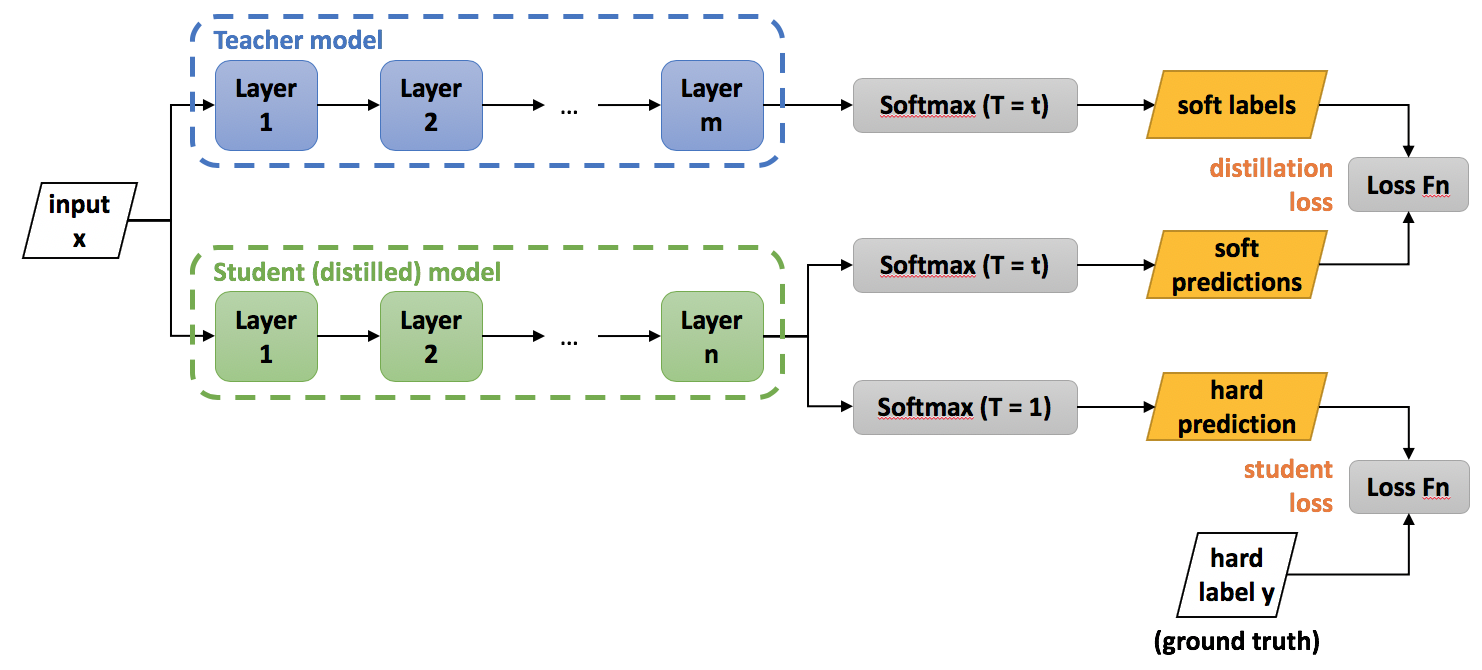
In distillation, knowledge is transferred from the teacher model to the student by using the class probabilities produced by the teacher as soft targets for the student.
However, in many cases, this probability distribution has the correct class at a very high probability, with all other class probabilities very close to 0. In distillation the temperature of the final softmax is raised until the teacher produces a suitable soft set of targets.
The probability \(p_i\) of class \(i\) is calculated from the logits \(z_i\) as:
\[p_i = \frac{exp\left(\frac{z_i}{T}\right)}{\sum_{j} \exp\left(\frac{z_j}{T}\right)}\]
where \(T\) is the temperature.
In the original paper by Hinton et al. the loss of the soft labels is combined with the loss of the hard labels/targets.
The overall loss function, incorporating both distillation and student losses is calculcated as:
\[\mathcal{L}(x;W) = \alpha * \mathcal{H}(y, \sigma(z_s; T=1)) + \beta * \mathcal{H}(\sigma(z_t; T=\tau), \sigma(z_s, T=\tau))\]
where \(x\) is the input, \(W\) are the student model parameters, \(y\) is the ground truth label, \(\mathcal{H}\) is the cross-entropy loss function, \(\sigma\) is the softmax function parameterized by the temperature \(T\), and \(\alpha\) and \(\beta\) are coefficients. \(z_s\) and \(z_t\) are the logits of the student and teacher respectively.
In general \(\tau\), \(\alpha\) and \(\beta\) are hyper parameters.
However, in many cases, this probability distribution has the correct class at a very high probability, with all other class probabilities very close to 0. In distillation the temperature of the final softmax is raised until the teacher produces a suitable soft set of targets.
The probability \(p_i\) of class \(i\) is calculated from the logits \(z_i\) as:
\[p_i = \frac{exp\left(\frac{z_i}{T}\right)}{\sum_{j} \exp\left(\frac{z_j}{T}\right)}\]
where \(T\) is the temperature.
In the original paper by Hinton et al. the loss of the soft labels is combined with the loss of the hard labels/targets.
The overall loss function, incorporating both distillation and student losses is calculcated as:
\[\mathcal{L}(x;W) = \alpha * \mathcal{H}(y, \sigma(z_s; T=1)) + \beta * \mathcal{H}(\sigma(z_t; T=\tau), \sigma(z_s, T=\tau))\]
where \(x\) is the input, \(W\) are the student model parameters, \(y\) is the ground truth label, \(\mathcal{H}\) is the cross-entropy loss function, \(\sigma\) is the softmax function parameterized by the temperature \(T\), and \(\alpha\) and \(\beta\) are coefficients. \(z_s\) and \(z_t\) are the logits of the student and teacher respectively.
In general \(\tau\), \(\alpha\) and \(\beta\) are hyper parameters.

What is the formula for the softmax function with temperature scaling?
\[\sigma(z_i;T) = \frac{exp\left(\frac{z_i}{T}\right)}{\sum_{j} \exp\left(\frac{z_j}{T}\right)}\]
Why do you need to use a softmax with a raised temperature when doing knowledge distillation?
Using a normal softmax, the correct class probability has often a very high probability, with all other class probability close to 0. As such, it doesn't provide much information beyond the ground truth labels already provided in the dataset.
Note: During inference the temperature is set back to 1.