Mixture-of-Experts with Expert Choice Routing
What new approach to MoE does Mixture-of-Experts with Expert Choice Routing introduce?
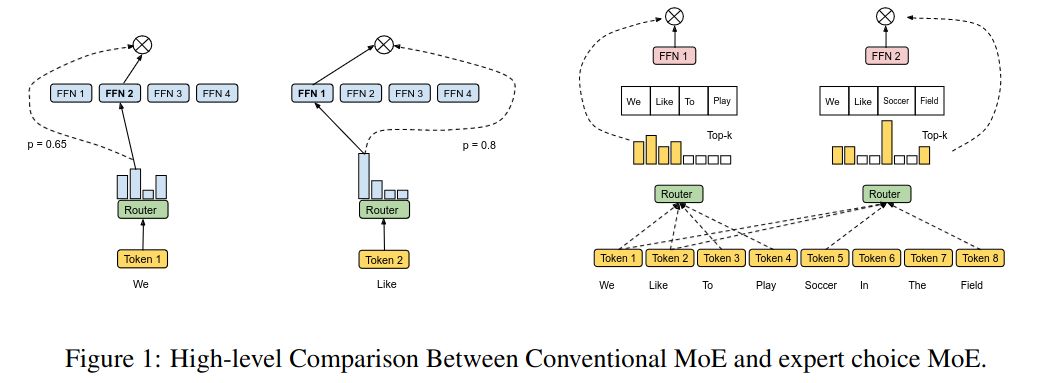
Expert Choice introduces a Mixture-of-Experts where instead of letting tokens select the top-\(k\) experts, the experts select the top-\(k\) tokens.

What advantage does Expert Choice bring to MoE?
The Expert Choice approach achieves perfect load balancing without additional loss functions.
How it routing done in Expert Choice MoE?
Given input matrix \(X \in \mathbb{R}^{n \times d}\) and \(e\) experts, the token-to-expert affinity scores are computed as:
\[S = \operatorname{Softmax}(X \cdot W_g), \text{where } W_g \in \mathbb{R}^{d \times e}, S \in \mathbb{R}^{n \times e}\]A token-to-expert assignment is represented by three matrices: \(I, G \in \mathbb{R}^{e\times k}\) and \(P \in \mathbb{R}^{e \times k \times n}\).
\(I[i,j]\) indicates which token is the \(j\)-th selected token of the \(i\)-th expert. \(P\) is the one-hot version of \(I\) and \(G\) is the gating matrix that stores the routing weights of the selected tokens.
\[G, I = \operatorname{TopK}(S^\top, k)\quad P = \operatorname{one-hot}(I)\]
\[S = \operatorname{Softmax}(X \cdot W_g), \text{where } W_g \in \mathbb{R}^{d \times e}, S \in \mathbb{R}^{n \times e}\]A token-to-expert assignment is represented by three matrices: \(I, G \in \mathbb{R}^{e\times k}\) and \(P \in \mathbb{R}^{e \times k \times n}\).
\(I[i,j]\) indicates which token is the \(j\)-th selected token of the \(i\)-th expert. \(P\) is the one-hot version of \(I\) and \(G\) is the gating matrix that stores the routing weights of the selected tokens.
\[G, I = \operatorname{TopK}(S^\top, k)\quad P = \operatorname{one-hot}(I)\]
How is \(k\) set in Expert Choice MoE?
\(k\) is set as \(k = \frac{n \times c}{e}\), where \(n\) is the total number ot tokens in the batch, \(c\) the capacity factor, and \(e\) the number of experts.
The paper used \(c = 2\) in most experiments, but showed that \(c = 1\) still outperformed the Switch Transformer. Even \(c = 0.5\) outperformed top-1 token choice gating as done in the Switch Transformer.
Should the number of experts per token be limited/regularized in Expert Choice Moe?
No.
The authors tried regularizing this but found it to decrease the performance.
The authors tried regularizing this but found it to decrease the performance.
What are the limitations of Expert Choice MoE?
It shares the limitation of most MoE methods: it requires large batch sizes.
AND it has a limitation unique to the expert choice approach: it does not work for auto-regressive text generation as the implementation needs to know the past and future tokens to perform the top-\(k\) selection.
AND it has a limitation unique to the expert choice approach: it does not work for auto-regressive text generation as the implementation needs to know the past and future tokens to perform the top-\(k\) selection.