Which base task does DUSt3R perform from which it can directly solve downstream tasks such as camera pose estimation, depth estimation, 3D reconstruction, etc..
Dense and Unconstrained Stereo 3D Reconstruction of arbitrary image collections.
Given a pair of images they regress the pointmaps. Where a pointmap is the a dense 2D field of 3D points associated with its corresponding RGB image.
Given a pair of images they regress the pointmaps. Where a pointmap is the a dense 2D field of 3D points associated with its corresponding RGB image.
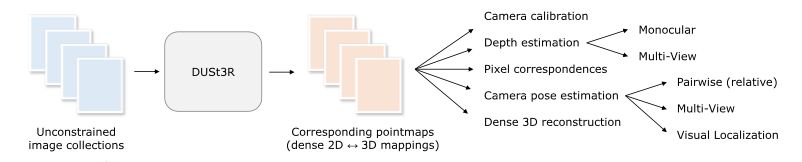
Give an overview of the DUSt3R architecture.
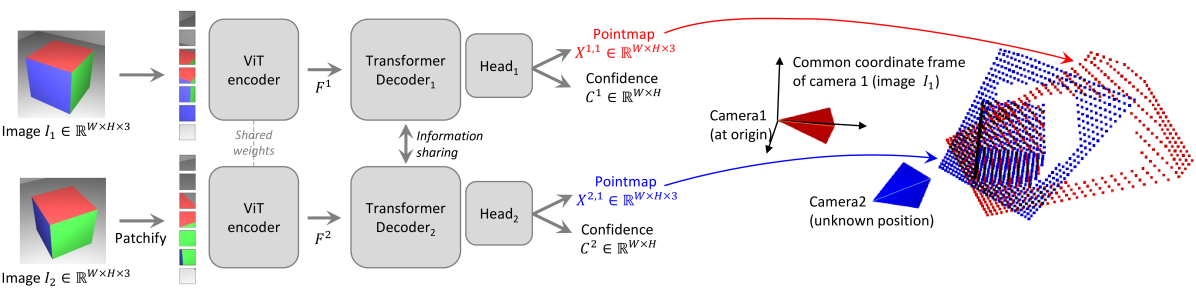
Two views of a scene \((I^1, I^2)\) are first encoded in a Siamese manner with a shared ViT encoder. The resulting token representations \(F^1\) and \(F^2\) are then passed to two transformer decoders that constantly exchange information via cross-attention.
Finally, two regression heads output the two corresponding pointmaps and associated confidence maps.
Importantly, the two pointmaps are expressed in the same coordinate frame of the first image \(I^1\).
The network architecture is inspired by CroCo: Self-Supervised Pre-training for 3D Vision Tasks by Cross-View Completion
What are the inputs and outputs of the DUSt3R network and what data do you need to setup this input/output?
The input is two input RGB images that correspond to two views of a scene: \(I^1, I^2 \in \mathbb{R}^{W\times H \times 3}\)
The outputs are the 2 corresponding pointmaps, expressed in the coordinate frame of \(I^1\): \(X^{1,1}, X^{2,1}\in \mathbb{R}^{W\times H \times 3}\) with associated confidence maps \(C^{1,1}, C^{2,1}\in \mathbb{R}^{W\times H \times 3}\).
To construct these outputs, you need to know the camera intrinsics \(K \in \mathbb{R}^{3 \times 3}\) , camera extrinsics (world-to-camera) \(P \in \mathbb{R}^{4 \times 4}\) and depthmap \(D \in \mathbb{R}^{W\times H}\).
pointmap \(X\) can be obtained by \(X_{i,j} = K^{-1} ([i D_{i,j}, j D_{i,j}, D_{i,j})\), where \(X\) is expressed in the camera coordinate frame.
To express pointmap \(X^n\) from camera \(n\) in camera \(m\)'s coordinate frame: \(X^{n,m} = P_m P_n^{-1} X^n\).
The outputs are the 2 corresponding pointmaps, expressed in the coordinate frame of \(I^1\): \(X^{1,1}, X^{2,1}\in \mathbb{R}^{W\times H \times 3}\) with associated confidence maps \(C^{1,1}, C^{2,1}\in \mathbb{R}^{W\times H \times 3}\).
To construct these outputs, you need to know the camera intrinsics \(K \in \mathbb{R}^{3 \times 3}\) , camera extrinsics (world-to-camera) \(P \in \mathbb{R}^{4 \times 4}\) and depthmap \(D \in \mathbb{R}^{W\times H}\).
pointmap \(X\) can be obtained by \(X_{i,j} = K^{-1} ([i D_{i,j}, j D_{i,j}, D_{i,j})\), where \(X\) is expressed in the camera coordinate frame.
To express pointmap \(X^n\) from camera \(n\) in camera \(m\)'s coordinate frame: \(X^{n,m} = P_m P_n^{-1} X^n\).
Which loss function is used to train DUSt3R?
Confidence-aware 3D Regression loss.
Given the ground-truth pointmaps \(\bar{X}^{1,1}\) and \(\bar{X}^{2,1}\) along with two corresponding sets of valid pixels \(\mathcal{D}^1,\mathcal{D}^2 \subseteq \{1\ldots W\}\times\{1\ldots H\}\) on which the ground-truth is defined.
The regression loss for a valid pixel \(i\in\mathcal{D}^v\) in view \(v\in\{1,2\}\) is simply defined as the Euclidean distance:
\[\mathcal{l}_{\text{reg}}(v,i) = (\| \frac{1}{z}X^{v,1}_{i} - \frac{1}{\bar{z}}\bar{X}^{v,1}_{i} )\|.\]
To handle the scale ambiguity between prediction and ground-truth, the predicted and ground-truth pointmaps are normalized by scaling factors \(z=\operatorname{norm}(X^{1,1},X^{2,1})\) and \(\bar{z}=\operatorname{norm}(\bar{X}^{1,1},\bar{X}^{2,1})\), respectively, which simply represent the average distance of all valid points to the origin:
\[\operatorname{norm}(X^1,X^2) = \frac{1}{|\mathcal{D}^1| + |\mathcal{D}^2|} \sum_{v \in \{1,2\}} \sum_{i \in \mathcal{D}^v} \| X^v_{i} \|\]As some parts of the image are harder to predict than others, the network also predicts a score for each pixel which represents the confidence that the network has about this particular pixel.
The final training objective is the confidence-weighted regression loss over all valid pixels:
\[\mathcal{L}_{\text{conf}} = \sum_{v \in \{1,2\}} \, \sum_{i \in \mathcal{D}^v} C^{v,1}_i \mathcal{l}_{\text{reg}}(v,i) - \alpha \log C^{v,1}_i\]
where \(C^{v,1}_i\) is the confidence score for pixel \(i\), and \(\alpha\) is a hyper-parameter controlling the regularization.
To ensure a strictly positive confidence, they define
\(C^{v,1}_i=1+\exp \widetilde{C^{v,1}_i} >1\).
This has the effect of forcing the network to extrapolate in harder areas, e.g. like those ones covered by a single view.
Training the network with this objective allows to estimate confidence scores without an explicit supervision.
Given the ground-truth pointmaps \(\bar{X}^{1,1}\) and \(\bar{X}^{2,1}\) along with two corresponding sets of valid pixels \(\mathcal{D}^1,\mathcal{D}^2 \subseteq \{1\ldots W\}\times\{1\ldots H\}\) on which the ground-truth is defined.
The regression loss for a valid pixel \(i\in\mathcal{D}^v\) in view \(v\in\{1,2\}\) is simply defined as the Euclidean distance:
\[\mathcal{l}_{\text{reg}}(v,i) = (\| \frac{1}{z}X^{v,1}_{i} - \frac{1}{\bar{z}}\bar{X}^{v,1}_{i} )\|.\]
To handle the scale ambiguity between prediction and ground-truth, the predicted and ground-truth pointmaps are normalized by scaling factors \(z=\operatorname{norm}(X^{1,1},X^{2,1})\) and \(\bar{z}=\operatorname{norm}(\bar{X}^{1,1},\bar{X}^{2,1})\), respectively, which simply represent the average distance of all valid points to the origin:
\[\operatorname{norm}(X^1,X^2) = \frac{1}{|\mathcal{D}^1| + |\mathcal{D}^2|} \sum_{v \in \{1,2\}} \sum_{i \in \mathcal{D}^v} \| X^v_{i} \|\]As some parts of the image are harder to predict than others, the network also predicts a score for each pixel which represents the confidence that the network has about this particular pixel.
The final training objective is the confidence-weighted regression loss over all valid pixels:
\[\mathcal{L}_{\text{conf}} = \sum_{v \in \{1,2\}} \, \sum_{i \in \mathcal{D}^v} C^{v,1}_i \mathcal{l}_{\text{reg}}(v,i) - \alpha \log C^{v,1}_i\]
where \(C^{v,1}_i\) is the confidence score for pixel \(i\), and \(\alpha\) is a hyper-parameter controlling the regularization.
To ensure a strictly positive confidence, they define
\(C^{v,1}_i=1+\exp \widetilde{C^{v,1}_i} >1\).
This has the effect of forcing the network to extrapolate in harder areas, e.g. like those ones covered by a single view.
Training the network with this objective allows to estimate confidence scores without an explicit supervision.