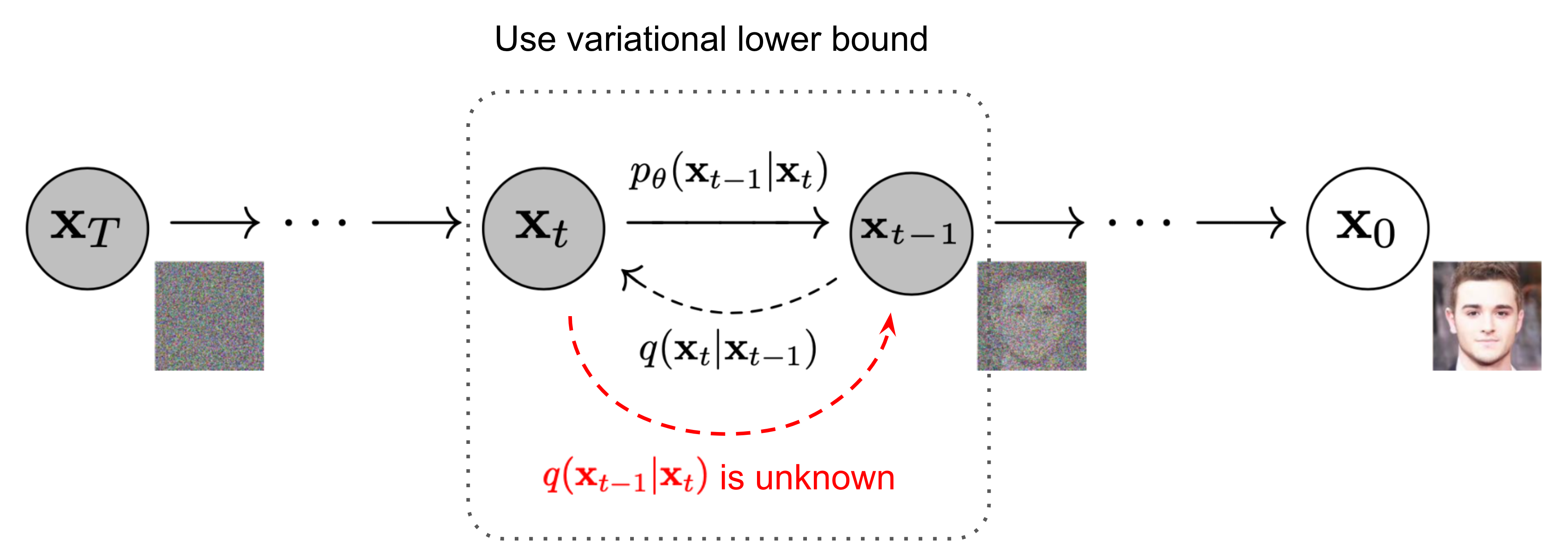
Diffusion Models

Given a data point sampled from a real data distribution \(\mathbf{x}_0 \sim q(\mathbf{x})\), let us define a forward diffusion process in which we add small amounts of Gaussian noise to the sample in \(T\) steps, producing a sequence of noisy samples \(\mathbf{x}_1, \dots, \mathbf{x}_T\). The step sizes are controlled by a variance schedule \(\{\beta_t \in (0, 1)\}_{t=1}^T\)
\[q(\mathbf{x}_t \vert \mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_t; \sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t\mathbf{I}) \]\[q(\mathbf{x}_{1:T} \vert \mathbf{x}_0) = \prod^T_{t=1} q(\mathbf{x}_t \vert \mathbf{x}_{t-1})\]As \(T \to \infty\), \(\mathbf{x}_T\) becomes equivalent to an isotropic Gaussian  distribution.

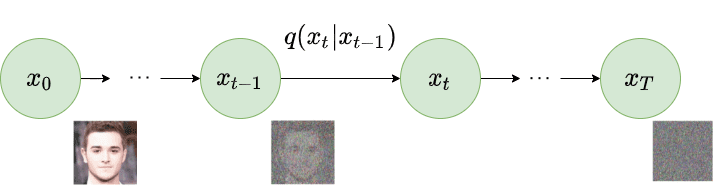
Forward diffusion process. Image modified by Ho et al. 2020

The scaling factor is needed to avoid making the variance of \(\mathbf{x}_t\) grow in each step.
If we would not scale it, after \(T\) steps we will have a value \(\mathbf{x}_t \in [-T,T]\).
To force \(\mathrm{Var}(x_1) = 1\) we need to scale by \(\sqrt{1 - \beta_t}\).

Using the reparameterization trick that tells us:
\[\begin{aligned} \mathbf{z} &\sim \mathcal{N}(\mathbf{z}; \boldsymbol{\mu}, \boldsymbol{\sigma^2}\boldsymbol{I}) & \\ \mathbf{z} &= \boldsymbol{\mu} + \boldsymbol{\sigma} \odot \boldsymbol{\epsilon} \text{, where } \boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \boldsymbol{I}) & \scriptstyle{\text{; Reparameterization trick.}} \end{aligned}\]If we define \(\alpha_t = 1 - \beta_t\) and \(\bar{\alpha}_t = \prod_{i=1}^t \alpha_i\):
\[\begin{aligned} \mathbf{x}_t &= \sqrt{\alpha_t}\mathbf{x}_{t-1} + \sqrt{1 - \alpha_t}\boldsymbol{\epsilon}_{t-1} & \text{ ;where } \boldsymbol{\epsilon}_{t-1}, \boldsymbol{\epsilon}_{t-2}, \dots \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \\ &= \sqrt{\alpha_t \alpha_{t-1}} \mathbf{x}_{t-2} + \sqrt{1 - \alpha_t \alpha_{t-1}} \bar{\boldsymbol{\epsilon}}_{t-2} & \text{ ;where } \bar{\boldsymbol{\epsilon}}_{t-2} \text{ merges two Gaussians (*).} \\ &= \dots \\ &= \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon} \\ q(\mathbf{x}_t \vert \mathbf{x}_0) &= \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t)\mathbf{I}) \end{aligned}\](*) Recall that when we merge two Gaussians with different variance, \(\mathcal{N}(\mathbf{0}, \sigma_1^2\mathbf{I})\) and \(\mathcal{N}(\mathbf{0}, \sigma_2^2\mathbf{I})\), the new distribution is \(\mathcal{N}(\mathbf{0}, (\sigma_1^2 + \sigma_2^2)\mathbf{I})\). Here the merged standard deviation is \(\sqrt{(1 - \alpha_t) + \alpha_t (1-\alpha_{t-1})} = \sqrt{1 - \alpha_t\alpha_{t-1}}\).

\[L_\text{simple} = L_t^\text{simple} + C\]
where \(C\) is a constant not depending on \(\theta\) and 
\[\begin{aligned} L_t^\text{simple} &= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}_t} \Big[\|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)\|^2 \Big] \\ &= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}_t} \Big[\|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)\|^2 \Big] \end{aligned}\]