Attention Is All You Need
Draw the general architecture of the Transformer model.
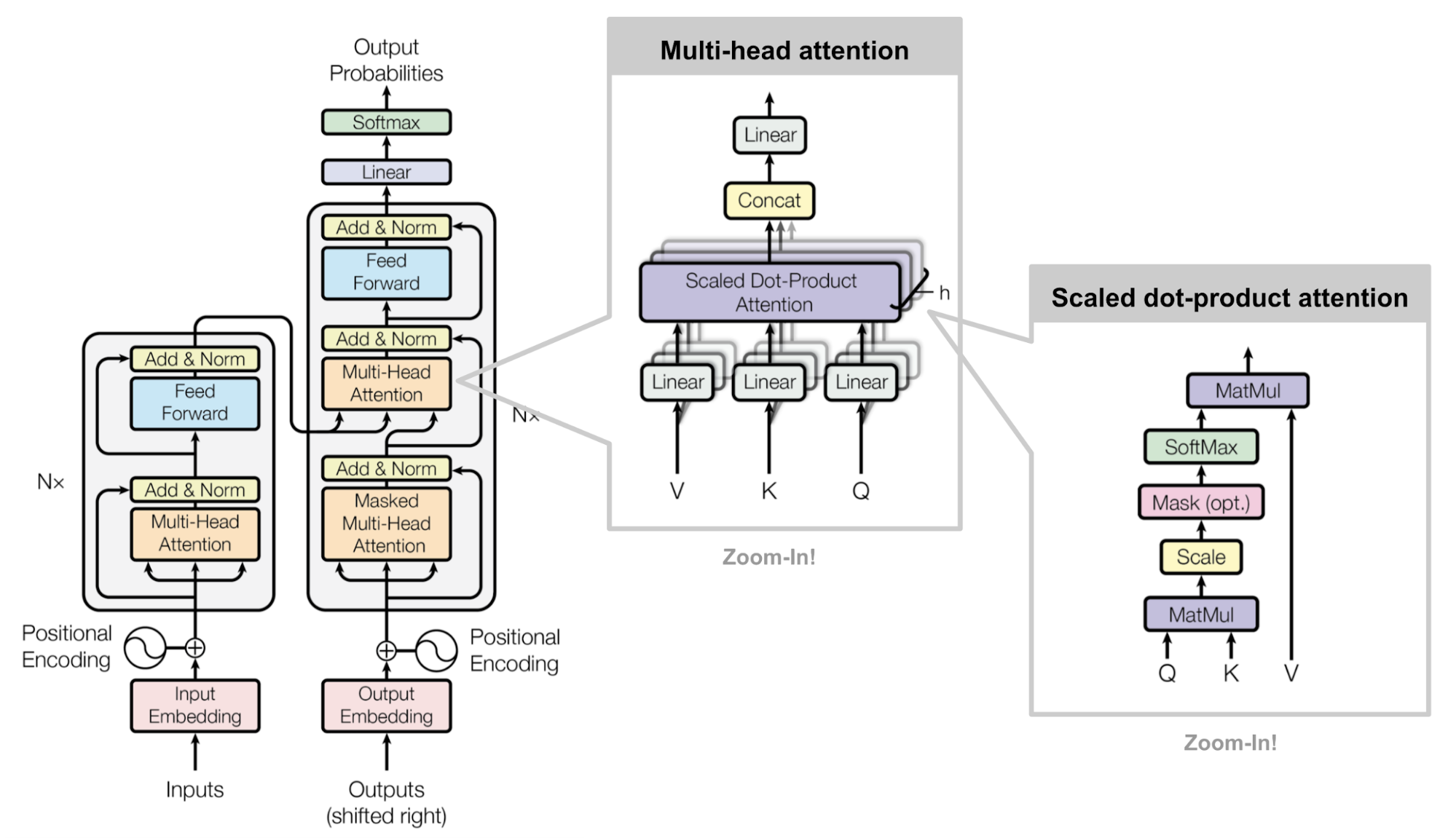
What is an attention function according to the "Attention is All you Need" paper?
An attention function can be described as mapping a query and a set of key-value pairs to an output, where the query, keys, values, and output are all vectors. The output is computed as a weighted sum of the values, where the weight assigned to each value is computed by a compatibility function of the query with the corresponding key.
The key/value/query concepts come from retrieval systems.
The attention operation turns out can be thought of as a retrieval process as well, so the key/value/query concepts also apply here.
What is Scaled Dot-Product Attention?
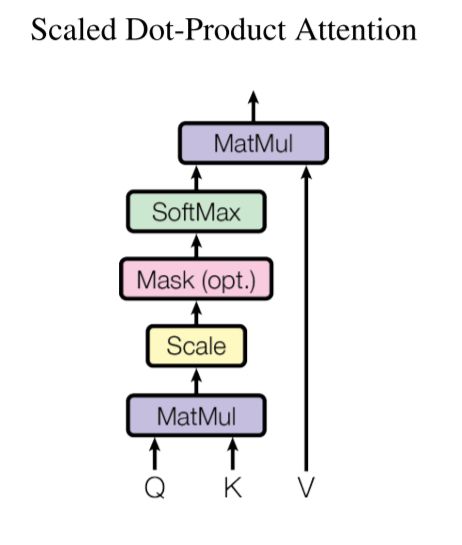
The input consists of queries and keys of dimension \(d_k\), and values of dimension \(d_v\). We compute the dot products of the query with all keys, divide each by \(\sqrt{d_k}\), and apply a softmax function to obtain the weights on the values.
In practice, attention function is computed on a set of queries simultaneously, packed together into a matrix \(Q\). The keys and values are also packed together into matrices \(K\) and \(V\). Compute the matrix of outputs as:
\[\mathrm{Attention}(Q, K, V) = \mathrm{softmax}(\frac{QK^T}{\sqrt{d_k}})V\]
What is Multi-Head Attention?
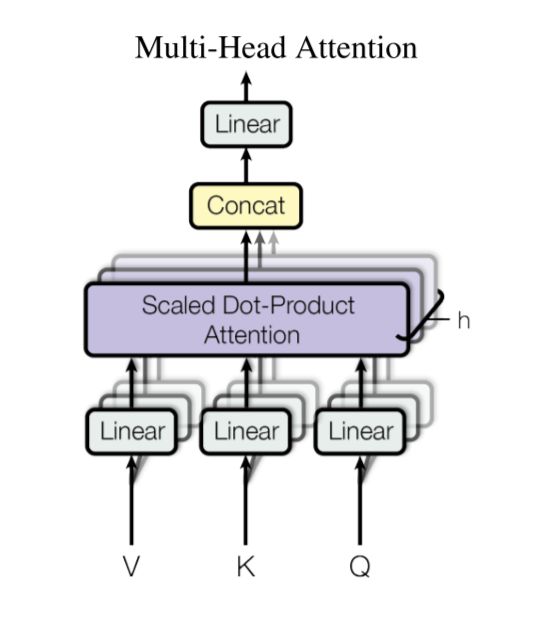
Instead of performing a single attention function with \(d_\text{model}\)-dimensional keys, values and queries, multi-head attention linearly project the queries, keys and values \(h\) times with different, learned linear projections to \(d_k\), \(d_k\) and \(d_v\) dimensions, respectively. On each of these projected versions of queries, keys and values it then performs the attention function in parallel, yielding \(d_v\)-dimensional output values. These are concatenated and once again projected, resulting in the final values, as
depicted above.
depicted above.
Multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions. With a single attention head, averaging inhibits this.
\[\mathrm{MultiHead}(Q, K, V) = \mathrm{Concat}(\mathrm{head_1}, ..., \mathrm{head_h})W^O \\ \text{where}~\mathrm{head_i} = \mathrm{Attention}(QW^Q_i, KW^K_i, VW^V_i)\]
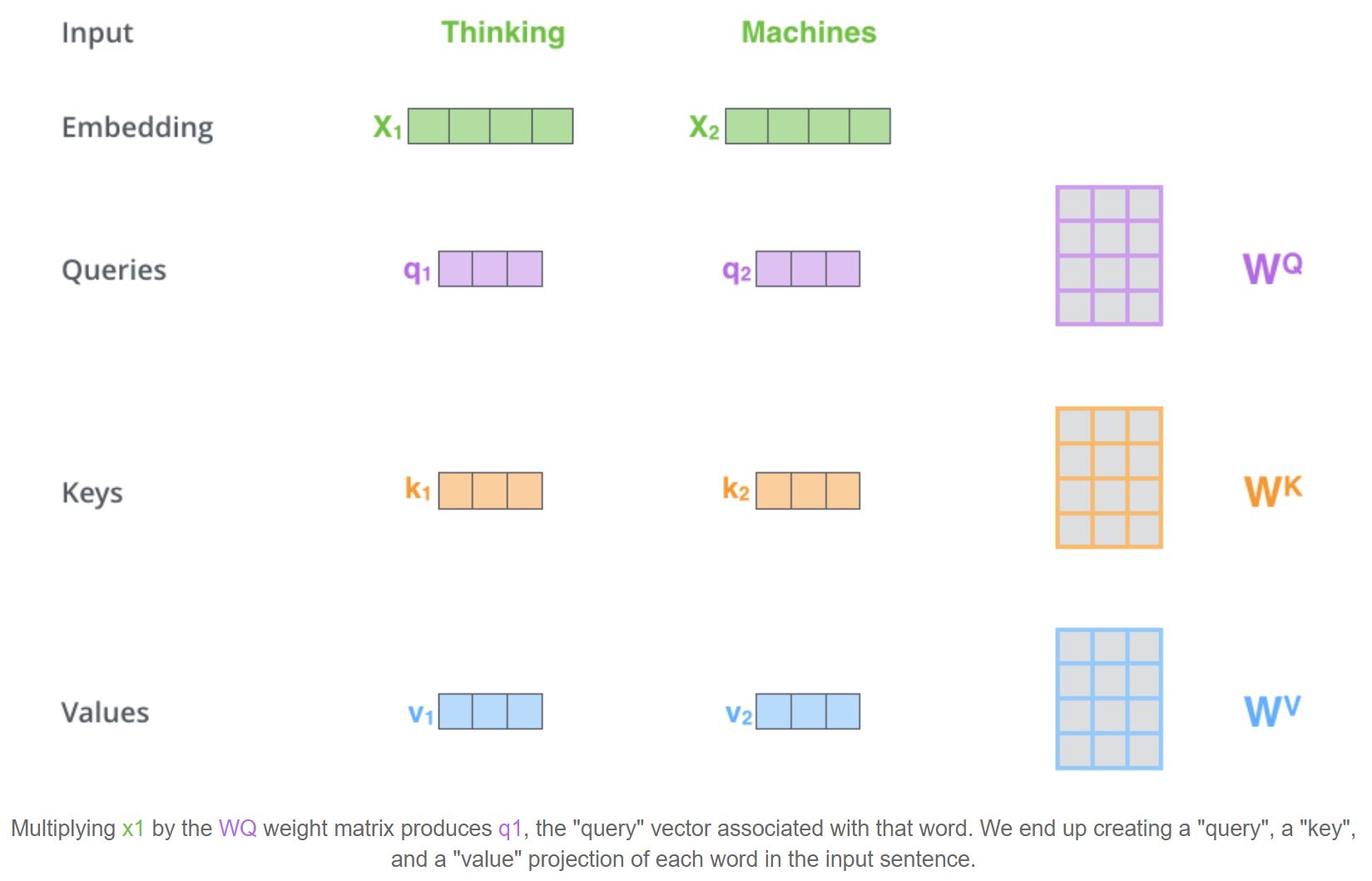
How do you get K, Q, V in Self-Attention?
These vectors are created by multiplying the embedding/input by three matrices that are learned during the training process.
Given an input matrix \(\mathbf{X} \in \mathbb{R}^{n \times d}\), \(\mathbf{Q} = \mathbf{X}\mathbf{W}_Q\), \(\mathbf{K} = \mathbf{X}\mathbf{W}_K\), and \(\mathbf{V} = \mathbf{X}\mathbf{W}_V\) are learned linear transformations of the input sequence.
Given an input matrix \(\mathbf{X} \in \mathbb{R}^{n \times d}\), \(\mathbf{Q} = \mathbf{X}\mathbf{W}_Q\), \(\mathbf{K} = \mathbf{X}\mathbf{W}_K\), and \(\mathbf{V} = \mathbf{X}\mathbf{W}_V\) are learned linear transformations of the input sequence.
What are the three different ways in which multi-head attention is used in Transformers?
1) The encoder contains self-attention layers. In a self-attention layer all of the keys, values and queries come from the same place, in this case, the output of the previous layer in the encoder. Each position in the encoder can attend to all positions in the previous layer of the encoder.
2) Similarly, self-attention layers in the decoder allow each position in the decoder to attend to all positions in the decoder up to and including that position. We need to prevent leftward information flow in the decoder to preserve the auto-regressive property. We implement this inside of scaled dot- product attention by masking out (setting to \(- \infty\)) all values in the input of the softmax which correspond to illegal connections.
3) In "encoder-decoder attention" layers, the queries come from the previous decoder layer, and the memory keys and values come from the output of the encoder. This allows every position in the decoder to attend over all positions in the input sequence
How are the feed forward layers used in the Transformer model?
In addition to attention sub-layers, each of the layers in our encoder and decoder contains a fully connected feed-forward network, which is applied to each position separately and identically. For this reason it's often called a Position-wise Feed Forward layer.
This layer consists of two linear transformations with a ReLU activation in between.
\[\mathrm{FFN}(x)=\max(0, xW_1 + b_1) W_2 + b_2\]
Another way of describing this is as two convolutions with kernel size 1.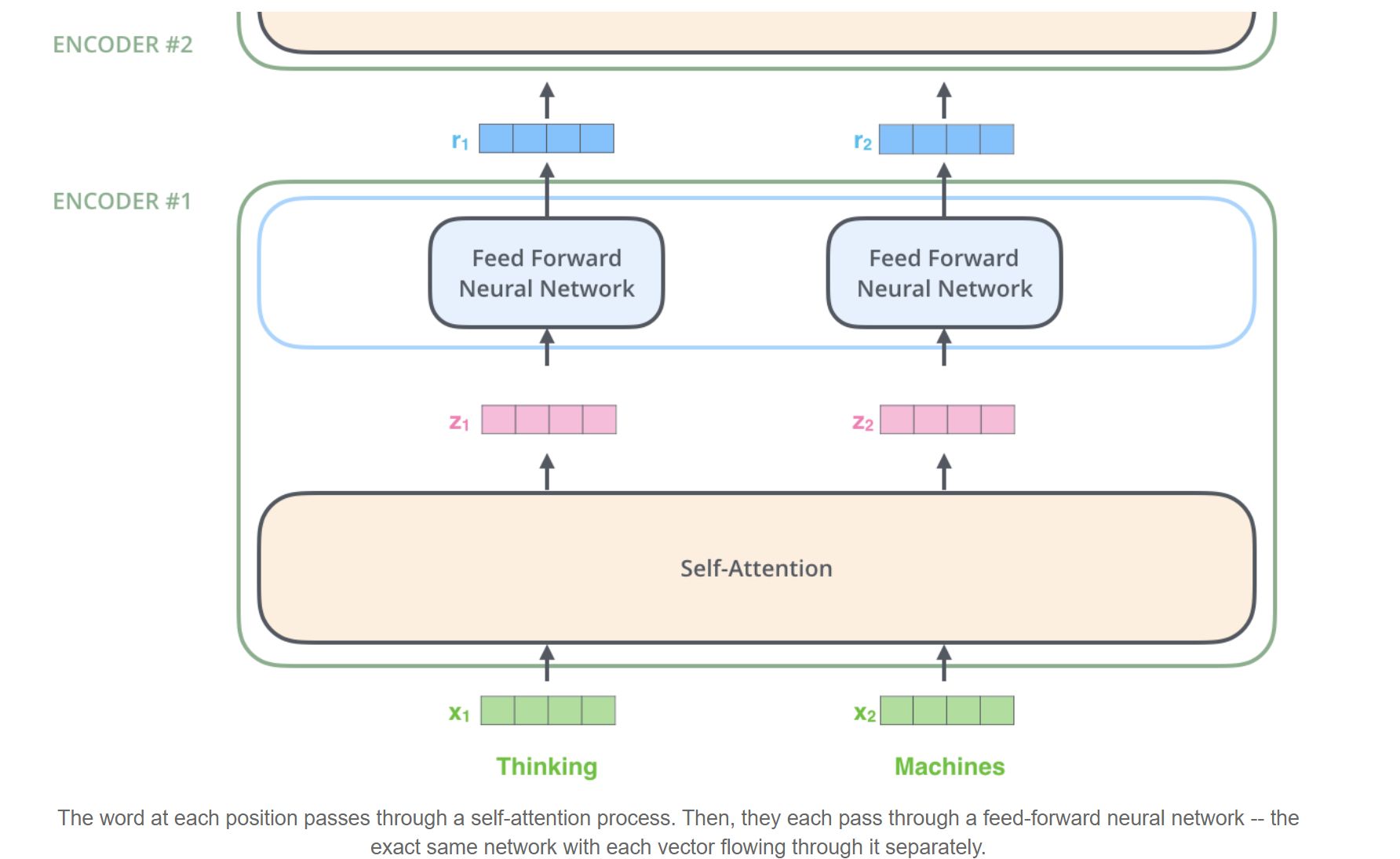

Give an overview of how the transformer model works during inference?
The encoder start by processing the input sequence. The output of the top encoder is then transformed into a set of attention vectors K and V. These are to be used by each decoder in its “encoder-decoder attention” layer which helps the decoder focus on appropriate places in the input sequence:
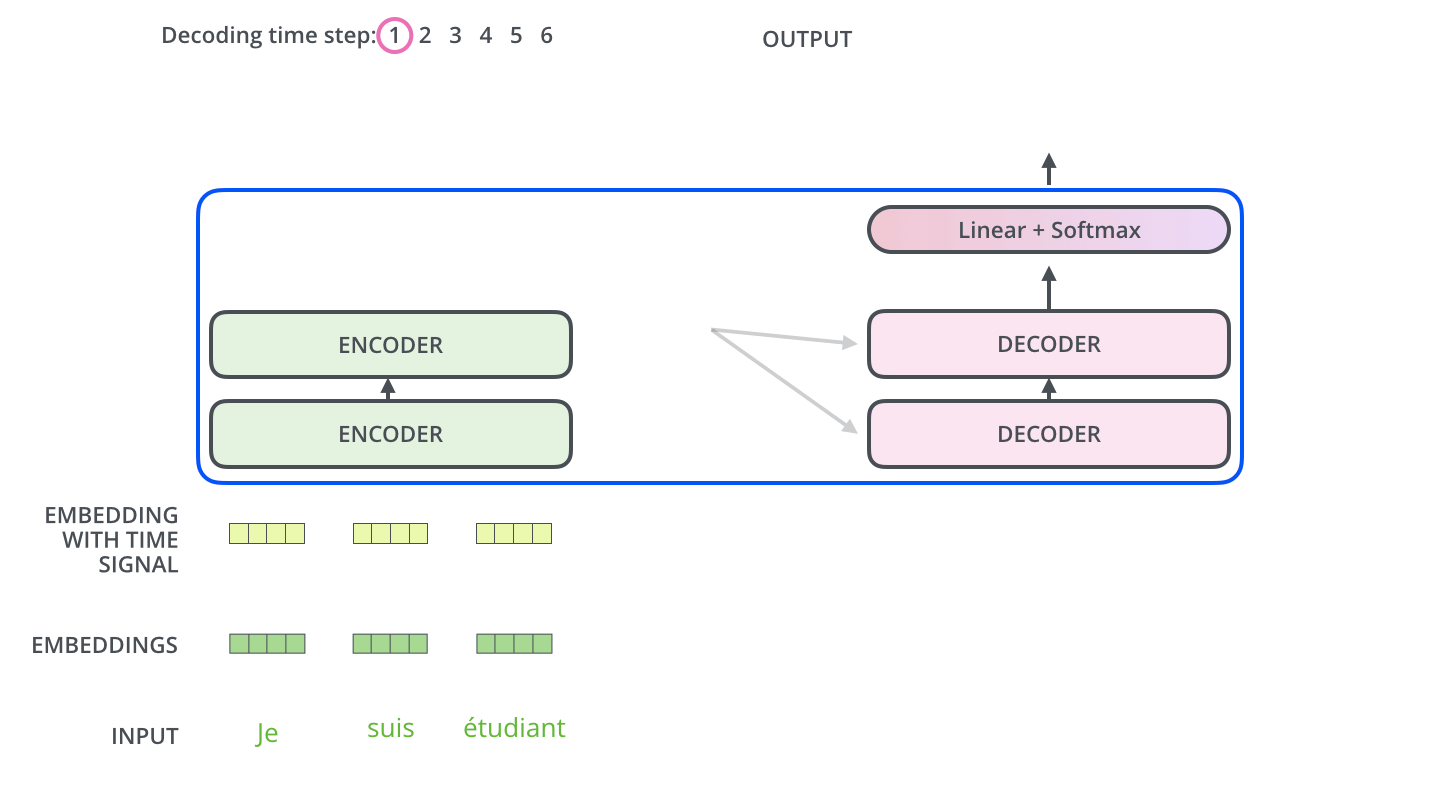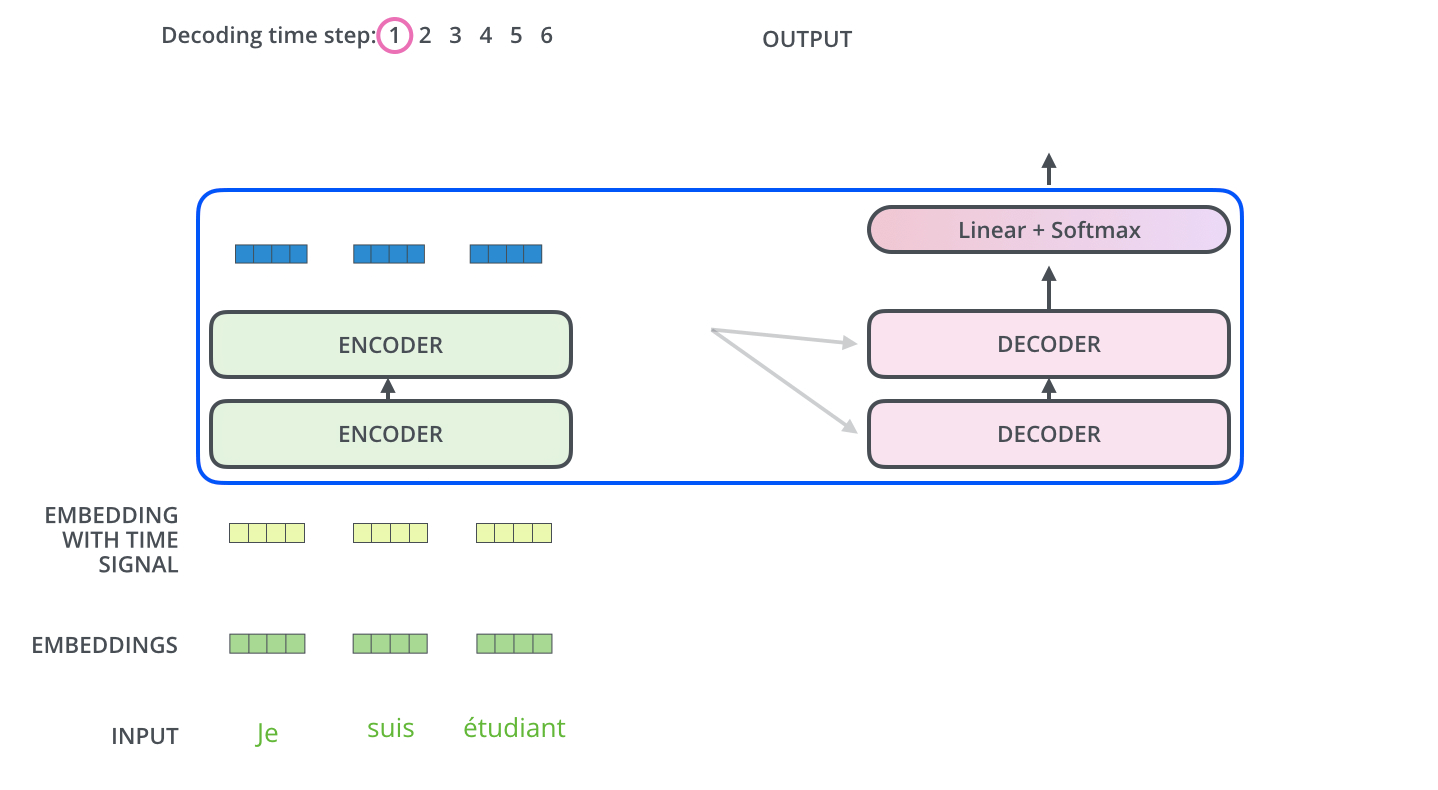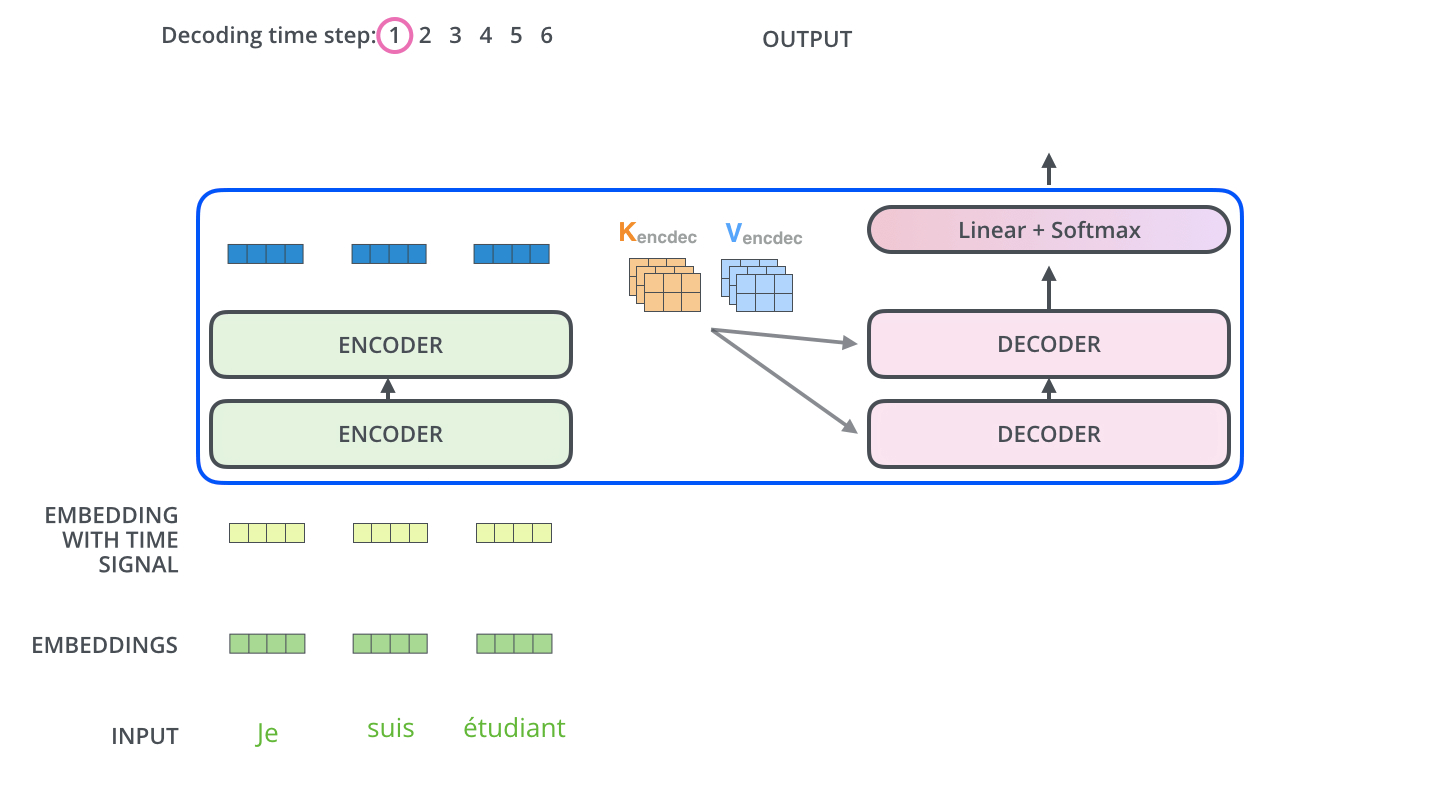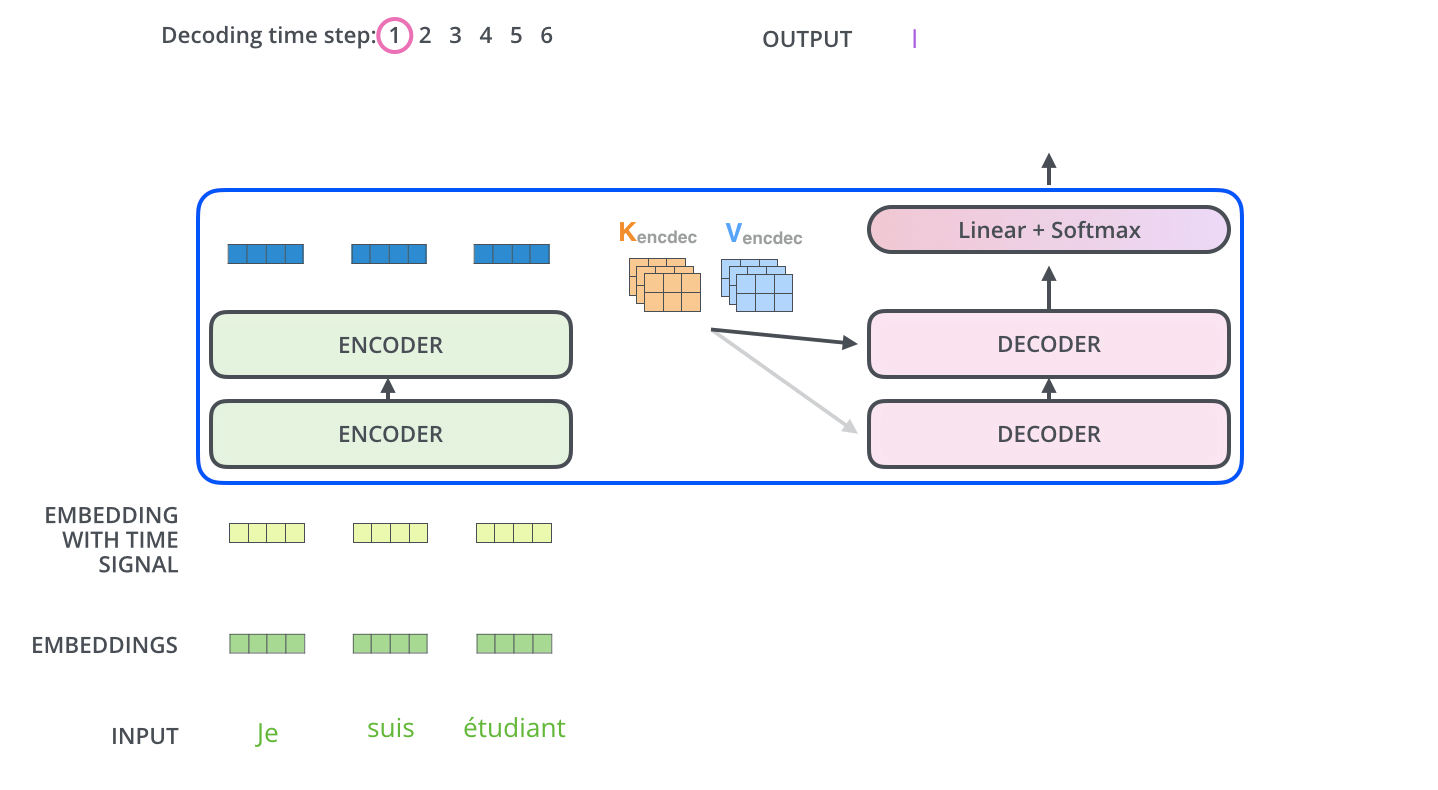
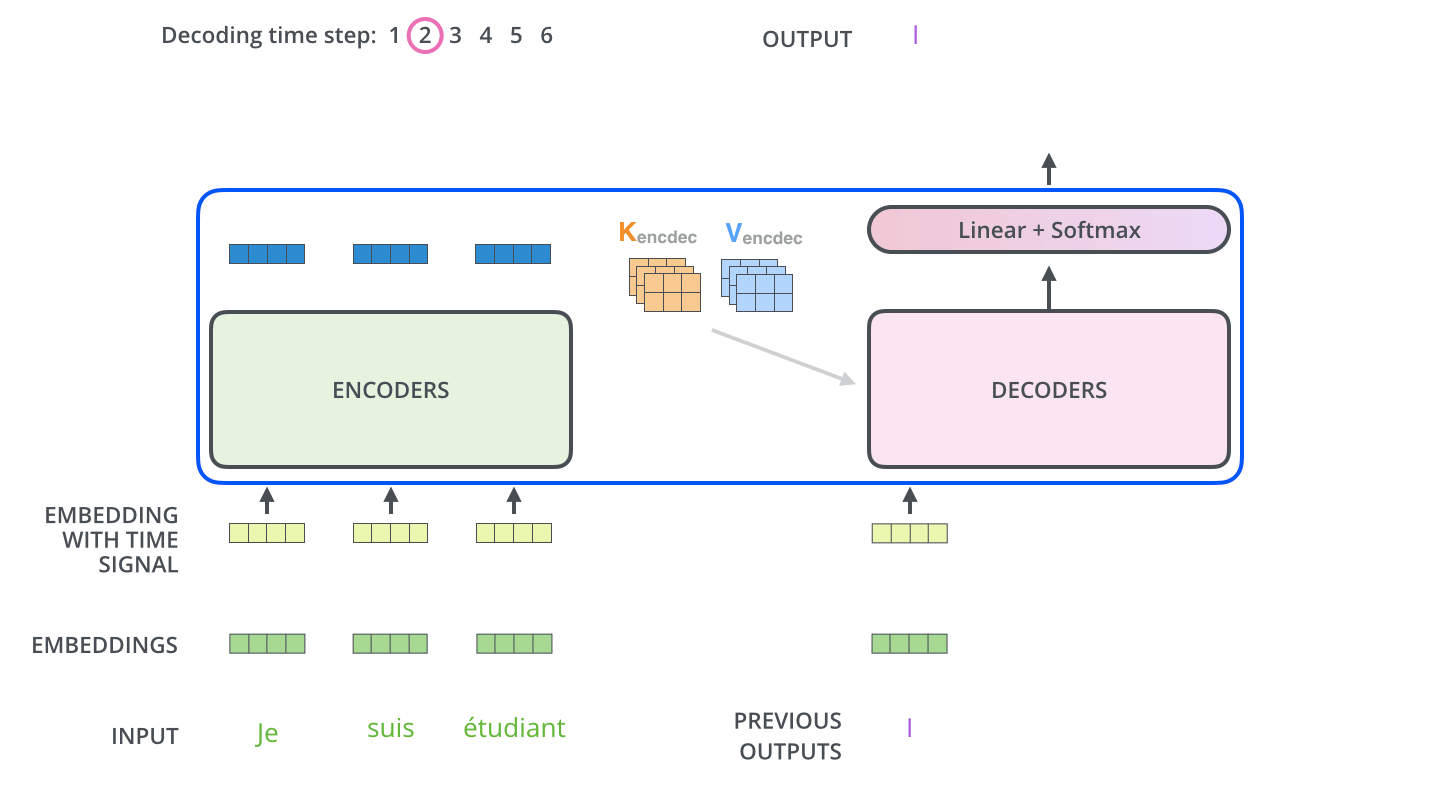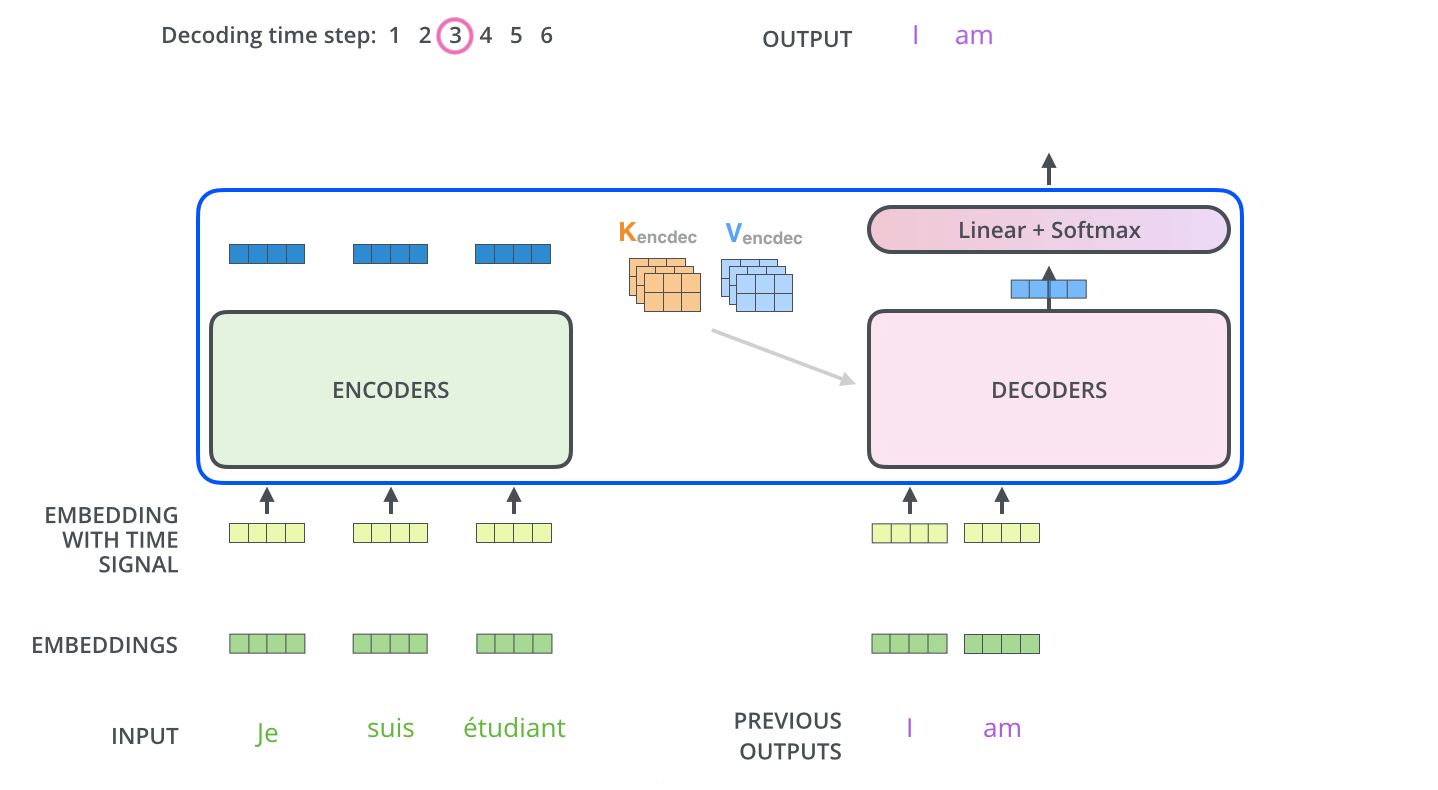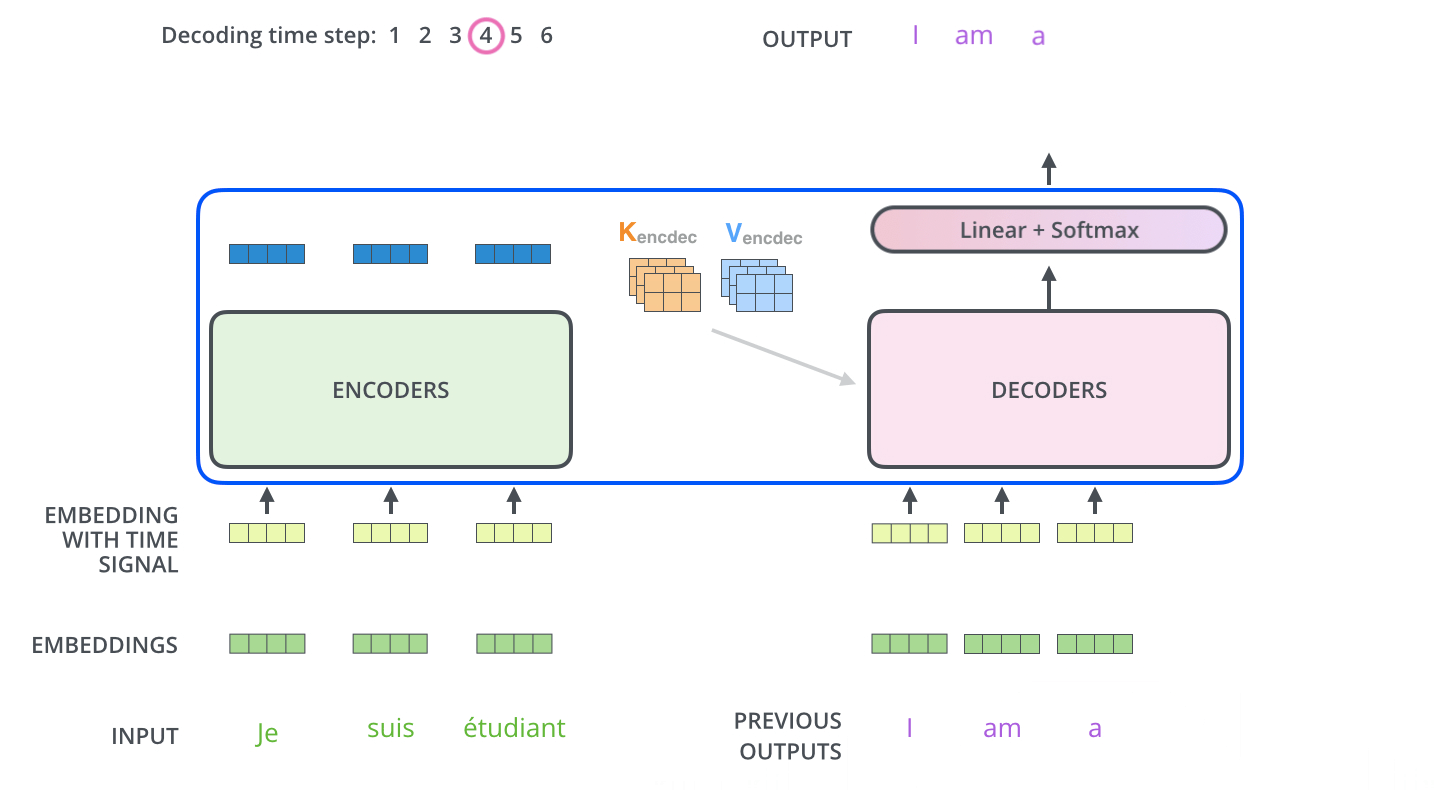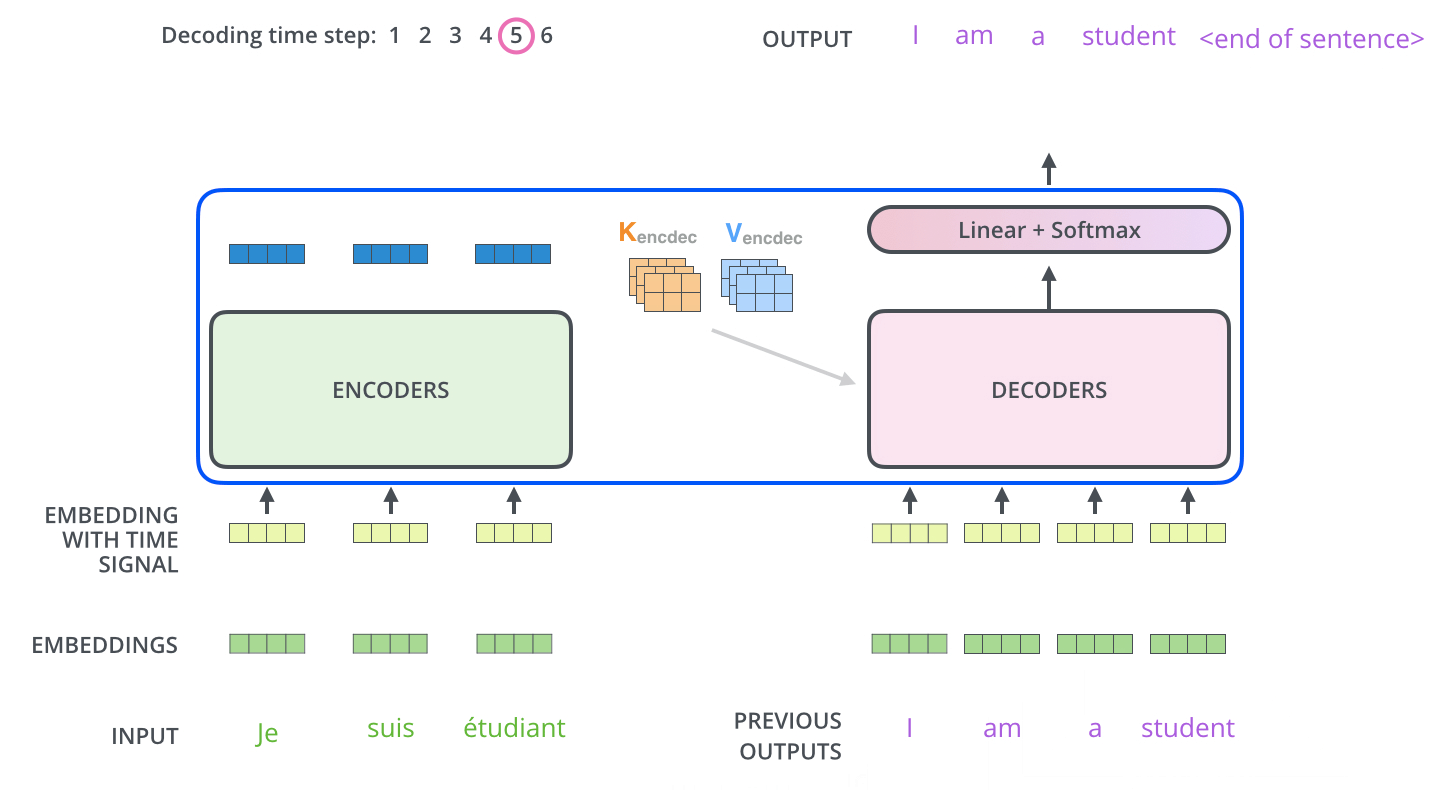
The following steps repeat the process until a special symbol is reached indicating the transformer decoder has completed its output. The output of each step is fed to the bottom decoder in the next time step, and the decoders bubble up their decoding results just like the encoders did. And just like we did with the encoder inputs, we embed and add positional encoding to those decoder inputs to indicate the position of each word.
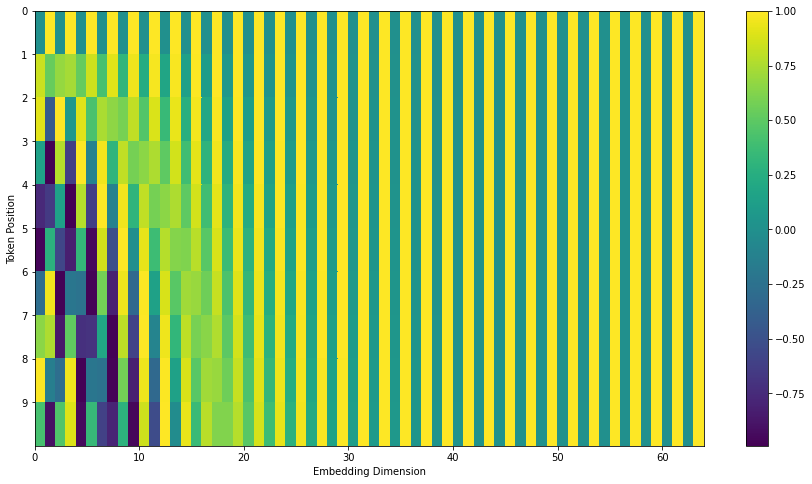
What are positional encodings in Transformers and why are they used?
Since the model contains no recurrence and no convolution, in order for the model to make use of the order of the sequence, we must inject some information about the relative or absolute position of the tokens in the sequence. To this end, we add “positional encodings” to the input embeddings at the bottoms of the encoder and decoder stacks. The positional encodings have the same dimension \(d_\text{model}\) as the embeddings, so that the two can be summed. There are many choices of positional encodings, learned and fixed.
In this work, they use sine and cosine functions of different frequencies: \(PE_{(pos,2i)} = sin(pos / 10000^{2i/d_{\text{model}}})\)
where \(pos\) is the position and \(i\) is the dimension.
Why are masks used in Transformers?
The purpose of masking is that you prevent the decoder state from attending to positions that correspond to tokens "in the future", i.e., those that will not be known at the inference time, because they will not have been generated yet.
At inference time, it is no longer a problem because there are no tokens from the future, there have not been generated yet.